STATISTICAL EVALUATION OF THE NEAR ATTACK CONFORMERS POPULATION
Otyepka Michal1, Banáš
Pavel1, Pytela Oldřich2, and Damborský Jiří3
1Department
of Physical Chemistry, Faculty of Science, Palacký
University, tř. Svobody 26, 771 46 Olomouc, Czech Republic
2Department
of Organic Chemistry, Faculty of Chemical Technology, University of Pardubice,
Čs. Legií 565, 532 10 Pardubice, Czech Republic
3National
Centre for Biomolecular Research, Masaryk University, Kotlářská 2, 611 37 Brno,
Czech Republic
The near
attack conformation (NAC) concept was introduced by Bruice et al. [1].
This concept proposes that the main reason for catalytic power of enzymes is
reduction of the configuration space of reacting atoms and bringing them
together to a typical arrangement defined as NAC. Bruice and coworkers revealed
linear relationship between log of relative rate constants (log krel)
and log of NAC population concluding that the rate constants are directly
dependent on the NAC population [1-3].
Haloalkane dehalogenases (HADs, EC 3.8.1.5) are bacterial enzymes
catalysing the cleavage of the carbon-halogen bond in haloorganic compounds by
a hydrolytic mechanism. The first step of the dehalogenation is SN2
attack of Asp124 carboxyl group oxygen to haloalkane carbon atom followed by AdN
of water molecule to ester intermediate. Bruice and coworkers postulated that
NAC of the substrate molecule positioned in the active site of HAD involves two
atoms forming the bond (Asp124-COO–…C-Cl).
These two atoms should ideally be within the van der Waals contact distance
(< 3.2 Å) and the attack angle (Asp124--COO–…C-Cl)
within ±15° deviation from the bonding angle in the TS for the SN2
displacement of Cl–. Here we propose effective tool for definition
and calculation of NAC or any other configuration subspace population in clear
statistical terms.
The NAC
configuration can be described in terms of geometrical parameters, e.g.
distances, angles, and dihedrals. Hence, the NAC configuration can be
characterized by n-dimensional vector m
made from selected n parameters. During the simulation the n
selected parameters make for each time step a realization of n-dimensional
stochastic vector n. If the system populates NAC, the realizations of
vector n fluctuate with n-dimensional Gauss distribution with
main value m and covariance matrix Σ. For
each MD simulation it is possible to test a hypothesis, whether the
parametrical vector is or isn’t in NAC. The hypothesis can be easily tested
using Mahalanobis distance representing a distance between NAC described by
vector m and snapshot configuration ni.
The Mahalanobis distance has 
Fisher-Snedecor distribution with n and N–n
degrees of freedom, where N is the number of steps in model simulation
used for covariance matrix Σ estimation, n is dimension of
vectors m and n, vector ni
denotes the vector n realization in i-th simulation snapshot.
Finally, the acceptation region for the hypothesis of snapshot being in NAC is
represent by an unequal
.
Presented method is based on testing the Mahalanobis distance of a
molecular arrangement from the NAC in the configuration space. The way to
estimate vector m as well as
matrix Σ will be discussed. Practical examples from the application
of developed method on quantitative estimation of NAC for HAD will be
presented.
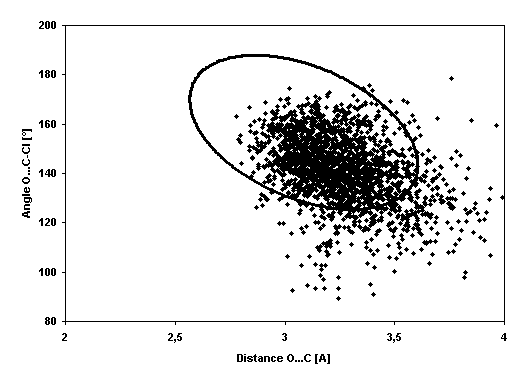
Plot of angle (Asp124--COO–…C-Cl)
against distance (Asp124-COO– … C-Cl)
for all HAD/chlorohexane complex MD simulation snapshots. The ellipse
represents critical Mahalanobis distance from NAC at which the hypothesis that
the configuration does not significantly differ from NAC is acceptable (the
point inside the ellipse can be considered as NAC conformation).
1. F. Lightstone, T.C. Bruice, J. Amer. Chem.
Soc., 118 (1996) 2595-2605
2. T.C. Bruice, F. Lightstone, Acc. Chem.
Res. 32 (1999) 127-136
3. T.C. Bruice, Acc. Chem. Res. 35 (2002)
139-148