XII. URČOVÁNÍ STRUKTURY KRYSTALŮ
1. Rentgenografické určení typu mříže
Typ mříže může být rentgenograficky určen přímým vyšetřením difrakčního záznamu, a to pomocí systematického vyhasínání reflexí určitých rovin.
Principiálně může být každá prostorová mříž popsána pomocí os vytvářejících primitivní buňku. Mřížové roviny oindexované vzhledem k této soustavě os splňující geometrické difarkční podmínky budou reflektovat rentgenové paprsky bez jakéhokoli omezení. Zvolíme-li však soustavu os základních translací tak, že elementární buňka je neprimitivní, a provedeme oindexování vzhledem k této nové soustavě os, budou reflexe od některých rovin chybět. Můžeme si to představit také jinak: vytvořme např. z primitivní mříže mříž prostorově centrovanou. Mřížové body přidané do středů buněk přidávají k původnímu vzoru novou periodicitu, nové translace. Pro některé typy rovin tak může vzniknout destruktivní interference odražených rentgenových paprsků v důsledku změny fázových vztahů. Původní primitivní mříž vykazuje reflexe od všech typů rovin, tedy např. i od sledů rovin (001).
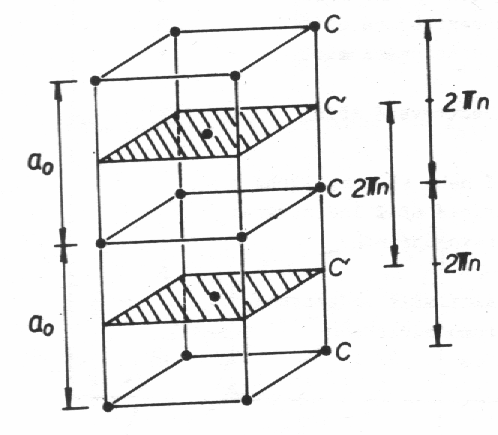 |
| Obr. 12.1. |
První řád reflexe odpovídá prvnímu interferenčnímu maximu, tj. fázovému rozdílu 2p vln odražených od sousedních rovin (roviny CC na obr. 12.1). Vložením dodatečných mřížových bodů do středů buněk se objeví mezi každým párem sousedních rovin CC nová rovina C'. Roviny C' jsou ekvivalentní s C, neboť jsou stejně obsazeny mřížovými body. Interferenční maximum prvního řádu (vzhledem k rovinám CC) se neobjeví, jelikož vlny odražené od rovin C a C' mají stejnou amplitudu a jsou právě v opačné fázi (posunuté o polovinu vlnové délky). Objeví se však silná reflexe reflexe druhého řádu, neboť vzdálenost CC odpovídá fázovému rozdílu 4p (dvě vlnové délky) a vzdálenost CC' rozdílu 2p (jedna vlnová délka). Obě odražené vlny budou tedy přesně ve fázi a budou se interferenčně skládat. Druhý řád reflexe od rovin původního sledu (001) je roven prvnímu řádu reflexe od sledu rovin (002); tj. sledu C, C', C, C', ... . V každém případě dojde k vymizení reflexe typu (001).
Veličina reprezentující závislost intenzity reflexe na krystalové struktuře se nazývá strukturní faktor* a značí se Fhkl. Výpočtem strukturních faktorů pro různé typy rovin ( hkl ) se dá ukázat, že u krystalů s prostorově centrovanou mříží vymizí všechny reflexy, jejichž součet indexů h+k+l není roven sudému číslu. Systematické vyhasínání reflexí může tedy sloužit k identifikaci typu mříže. Přehled systematických vyhasínání reflexí je uveden v tabulce 12.1.
| třída reflexí | podmínky pro nevyhasínání (n = celé číslo) | interpretace vyhasnutí ostatních reflexí | symbol typu mříže |
| hkl | h + k + l = 2n | prostorově centrovaná mříž | I |
| h + k = 2n | stěnově centrovaná mříž | C | |
| h + l = 2n | stěnově centrovaná mříž | B | |
| k + l = 2n | stěnově centrovaná mříž | A | |
| h + k = 2n h + l = 2n k + l = 2n | plošně centrovaná mříž | F | |
| -h + k + l = 3n | romboedrická mříž indexovaná pomocí hexagonálního systému os | R | |
| h + k + l = 3n | hexagonální mříž indexovaná pomocí romboedrického systému os | H |
Poznámka:
Nutno zdůraznit, že počet reflexí daného krystalu je stejný, ať popíšeme jeho mříž
pomocí primitivní nebo centrované buňky. "Chybějící reflexe" v případě popisu centrovanou buňkou
jsou pouze důsledek nového indexování. Hypotetický příklad "předělání" primitivní mříže na centrovanou
vložením dalších mřížových bodů by však vedl ke skutečné změně počtu reflexí.
2. Laueho grupy symetrie krystalu
U Laueho metody*
jsme se zmínili o tom, že v případech, kdy se primární svazek šíří krystalem
podél určité osy symetrie nebo podél roviny zrcadlení, je rozmístění difrakčních stop na
lauegramu symetrické. Je však nutno respektovat další skutečnost: symetrie svazku difraktovaných paprsků
bude vyšší nežli symetrie krystalu, a to o střed symetrie. Podle Friedelova zákona
je totiž intenzita "reflexe" od sledů rovin ( h k l ) a ( -h -k -l ) stejná, tj.
rentgenové paprsky "nerozlišují", zda protilehlé soustavy rovin jsou nebo nejsou sdruženy podle
středu symetrie. Na obr. 12.2 jsou pro ilustraci znázorněny čtyři roviny krystalu s 2četnou osou
podél c. Z operací symetricky 2četné osy je zřejmé, že symetricky ekvivalentní jsou:
rovina ( h k l ) s rovinou ( -h -k l ) a rovina ( h k -l ) s rovinou
( -h -k -l ). Jsou tudíž ekvivalentní v těchto dvojicích, nikoli však všechny čtyři navzájem.
Kdybychom zhotovili dva difrakční snímky krystalu podél osy c, jednou v kladném
a podruhé v záporném smyslu osy, získali bychom v důsledku platnosti Friedelova zákona dva totožné
difraktogramy. Krystal by se tudíž jevil tak, jako by roviny ( h k l), ( -h -k l ),
( h k -l ) a ( -h -k -l ) byly všechny vzájemně ekvivalentní, tj. jako by krystal
měl střed symetrie. Podobně by se takto jevil i krystal mající pouze rovinu symetrie. A úplně
stejně by difraktoval rentgenové záření i krystal s 2četnou osou a k ní kolmou rovinou symetrie,
který jediný z uvedených případů má skutečně střed symetrie ( v důsledku kombinace 2 a m ).
Difrakční symetrie krystalů s bodovými grupami 2, m a 2/m jsou tedy totožné a samotnou difrakcí
rentgenových paprsků nelze tyto bodové grupy rozlišit.
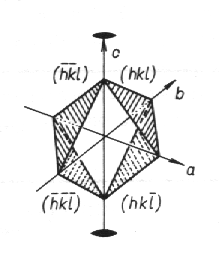 |
| Obr. 12.2 Ze symetrie difrakčního obrazu lze určit Laueho grupu symetrie; krystal obsahující pouze dvojčetnou osu má Laueho grupu 2/m. |
Bodové grupy, které se navzájem liší jen přítomností či nepřítomností inverze (a prvky symetrie,
které vznikly v důsledku přítomnosti této inverze) zahrnujeme do téže Laueho grupy.
Její symbol je dán symbolem té grupy, která má střed symetrie. Lauehových grup je celkem 11 a jsou
uvedeny v tabulce 12.2.
| Laueho grupy | obsažené bodové grupy |
| 2/m | 2, m, 2/m |
| mmm | 222, mm2, mmm |
| 4/m | 4, 4i, 4/m |
| 4/mmm | 422, 4mm, 4i2m, 4/mmm |
| 3i | 3, 3i |
| 3im | 32, 3m, 3im |
| 6/m | 6, 6i, 6/m |
| 6/mmm | 622, 6mm, 6im2, 6/mmm |
| m3i | 23, m3i |
| m3im | 432, 4i3m, m3im |
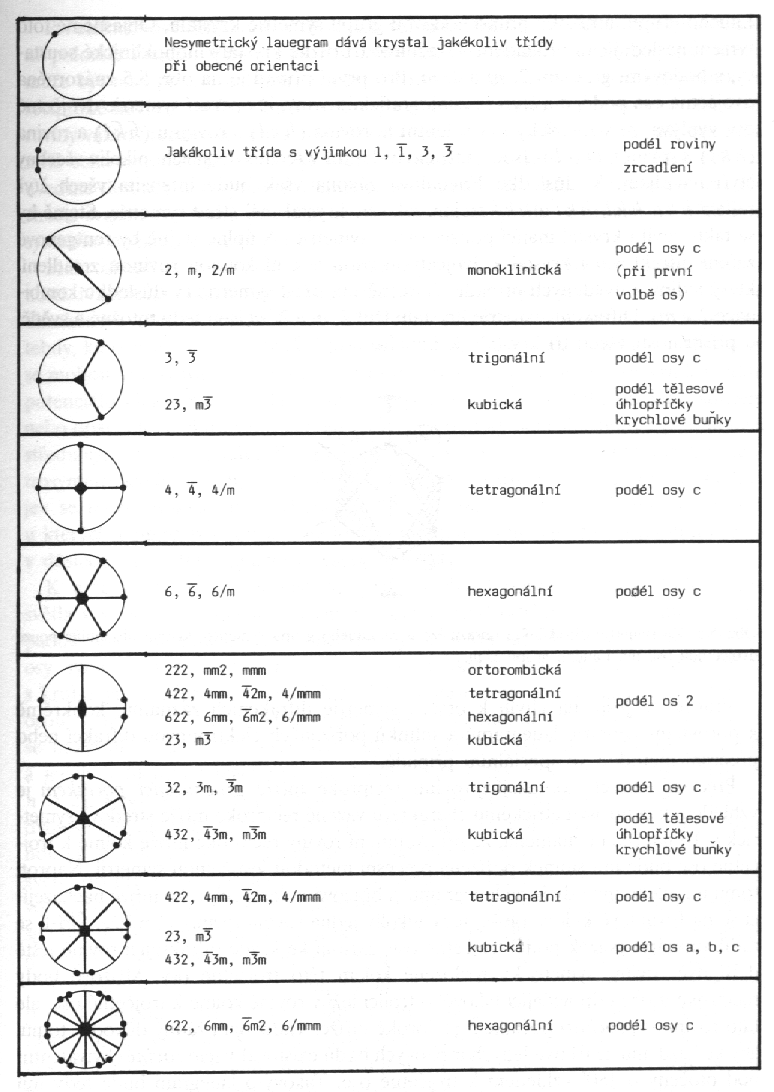 |
| Obr. 12.3 Deset možných typů z hlediska symetrie. |
Na obrázku 12.3 jsou znázorněny možné typy lauegramů. Symetrické lauegramy vykazují v rovině snímku souměrnost odpovídající osám nebo rovinám symetrie krystalu, které při difrakci leží podél primárního paprsku, a tedy kolmo k rovině snímku (obr. 12.4). Z hlediska souměrnosti existuje pouze 10 možných typů lauegramů. Pro každý typ jsou na obr. 12.3 uvedeny též krystalové třídy a orientace krystalů vedoucí k danému typu lauegramu. Naopak je zřejmé, že symetrické lauegramy mohou sloužit také při určování nebo potvrzování symetrie krystalů.
 |
| Obr. 12.4 Trojčetná symetrie difrakčního záznamu podél osy 3i. |
3. Určování prostorových grup
V podkapitole XII.1 (Určení typu mříže) jsme rozebírali systematické vyhasínání
některých reflexí v důsledku subtranslací přítomných v centrovaných mřížích. Subtranslace
jsou též součástí některých složených prvků symetrie, konkrétně šroubových os
a skluzových rovin.
Jako příklad vyšetřujme krystal, jehož bodová grupa obsahuje 4četnou osu, rovnoběžnou s c. Tato 4četná osa může být v prostorové grupě reprezentována osami 4, 41, 42 nebo 43. Má-li prostorová grupa osu 4, je vzdálenost rovin (001) rovna řádné mřížové translaci podél osy c. Je-li však přítomna osa 41, pak její translační složka opakuje tyto roviny ve vzdálenosti c/4. Čtyřčetná osa 42 opakuje roviny (001) ve vzdálenostech c/2 a osa 43 ve vzdálenostech 3c/4 = -c/4, tj. opět ve vzdálenostech c/4. Je-li tudíž ze symetrie bodové grupy známo, že krystal obsahuje 4četnou osu podél c, projeví se její charakter ve vzdálenostech rovin kolmých k této ose, zde tedy rovin (001).
Existence subtranslačních rovin v důsledku přítomnosti šroubových os nebo skluzových rovin se při difrakci rentgenových paprsků projeví podobně jako přítomnost nevrcholových mřížových bodů v centrovaných buňkách: systematickou nepřítomností (vyhasnutím) některých reflexí. Pouze primitivní mříž s čistými rotačními osami a čistými rovinami zrcadlení neklade omezující podmínky pro výskyt reflexí. Vyšetřováním strukturních faktorů* pro různé typy reflexí je možné sestavit přehled systematicky vyhasínajících reflexí (viz tab. 12.3). V tomto přehledu jsou pro určité třídy reflexí uvedeny podmínky, které vedou k výskytu reflexí této třídy, nebo-li k vyhasnutí reflexí nesplňujících tyto podmínky. Každá podmínka vyplývá z přítomnosti některé skluzové roviny nebo šroubové osy. (V tabulce je za symbolem prvku symetrie uveden v závorce typ mříže.)
 |
Srovnáním tabulek 12.1 a 12.3 zjistíme, že systematická vyhasnutí určitých reflexí obecných typů rovin hkl charakterizují centrované translační mříže, systematická vyhasnutí určitých reflexí třídy hk0, h0l, 0kl vyznačují přítomnost skluzových rovin a systematická vyhasnutí reflexí třídy h00, 0k0, 00l značí přítomnost šroubových os.
Při analýze systematicky vyhasínajících reflexí je však třeba mít na paměti, že vyhasínání reflexí obecnějšího typu má za následek vyhasínání některých reflexí méně obecného typu. Například vyhasínání reflexí obecného typu u krystalů s prostorově centrovanou mříží pro h + k + l = 2n±1 má automaticky za následek vyhasínání reflexí h00 pro lichá h. Nepřítomnost těchto reflexí tudíž nemůže sloužit jako indikace výskytu šroubové osy 21 podél a. Na druhé straně, jsou-li například pozorovány reflexe 0kl s lichými hodnotami indexu k, znamená to pouze, že krystal neobsahuje skluzovou rovinu b. Jiné závěry o přítomnosti nebo nepřítomnosti dalších prvků symetrie, zde například o výskytu roviny zrcadlení místo skluzové roviny b, nelze z výskytu těchto reflexí odvozovat.
Při hledání prostorové grupy symetrie krystalu můžeme
z difarkčních experimentů určit pouze
- Laueho grupu symetrie,
- typ mříže,
- přítomnost šroubových os a skluzových rovin.
Tyto informace jsou shrnuty v difrakčním symbolu krystalu, který sestává ze symbolu Laueho grupy, ze symbolu pro typ mříže a dále ze symbolů šroubových os či skluzových rovin identifikovatelných ze systematického vyhasínání reflexí a uspořádaných ve stejné posloupnosti význačných směrů jako u prostorových grup dané krystalové soustavy. Uveďme například tři následující difrakční symboly a prostorové grupy symetrie krystalů, které mají stejnou difrakční symetrii:
| mmmI--- | obsahuje grupy Imm2, I222, I212121, Immm, | |
| mmmI-a- | obsahuje grupy Ima2, Imam, | |
| mmmIbca | obsahuje pouze grupu Ibca. |
Pomlčky značí, že v daných význačných směrech uvažovaného ortorombického krystalu neleží žádné šroubové osy ani skluzové roviny kolmé k těmto směrům. Je patrné, že pouze v posledním případě je prostorová grupa krystalu určena difrakčním symbolem jednoznačně. Celkem existuje 122 různých difrakčních symbolů pro 230 prostorových grup. Pouze v 50 případech určuje difrakční symbol pouze jedinou prostorovou grupu a v 72 případech odpovídá difrakční symbol více než jedné prostorové grupě.
K upřesnění prostorové grupy lze v nejednoznačných případech použít dalších metod, většinou umožňujících určit, zda se jedná nebo nejedná o krystal se středem symetrie, případně prokázat absenci roviny zrcadlení. K těmto metodám patří metody využívající chemických informací, určování bodových grup nedifrakčními prostředky, studium rozdělení intenzit reflexí, vyšetřování maxim v Pattersonově syntéze a aplikace jevu anomální disperze. Pomocí těchto metod lze jednoznačně identifikovat 204 prostorových grup z 230. Zbývající grupy jsou především páry enantiomorfních prostorových grup.