IX. PORUCHY KRYSTALOVÝCH STRUKTUR

   Doposud v úvahách o krystalové struktuře jsme předpokládali, že atomy (ionty) jsou pravidelně uspořádány. Uvažovali jsme vlastně ideální krystal, který si představujeme jako nekonečné opakování strukturních jednotek v prostoru. Ve skutečnosti se však nikdy s tak dokonalou strukturou nesetkáme. Právě naopak. V reálných krystalech se vždy vyskytují určité odchylky od ideální periodické krystalové struktury. Každou takovou odchylku nazýváme porucha. Velmi často a obvykle dělíme poruchy krystalové mřížky do několika skupin podle toho, v kolika dimenzích se jejich rozměry liší od rozměrů atomů. Podle této geometrické klasifikace rozlišujeme poruchy bodové, čárové, plošné a objemové. Mnohé vlastnosti reálných krystalů, které jsou vždy nedokonalé, jsou velmi silně závislé na množství a druhu poruch krystalové struktury. Jejich studium má proto zásadní význam pro mnohé oblasti fyziky pevných látek a materiálového výzkumu. V dalším si všimneme jednotlivých skupin poruch. Nebudeme si však všímat okamžitých odchylek v polohách částic (např. tepelné kmity).

    1. Bodové poruchy

   Různé typy bodových poruch jsou schématicky znázorněny na obrázku 9.1. Substitučně nebo intersticiálně zabudovaný cizí atom jsou na obr. 9.1a a 9.1b. Chybějící atom - vakance - je znázorněn na obr. 9.1c. Kombinace intersticiální poruchy a vakanční poruchy vznikne přemístěním atomu z řádné polohy v mříži do polohy intersticiální a nazývá se Frenkelova porucha (obr. 9.1d). Schottkyho porucha (obr. 9.1e) se vyskytuje v iontových krystalech: kationtová vakance je vyvážena aniontovou vakancí, obě poruchy tvoří společný pár. Je zřejmé, že v okolí poruch dojde k dalším lokálním vysunutím atomů z řádných mřížových poloh. Tato skutečnost může být také interpretována jako lokální deformace mříže a bývá znázorňována deformací sítě mřížových čar. U molekulárních krystalů může být povaha bodových poruch složitější v důsledku možných nepravidelných poloh molekul.

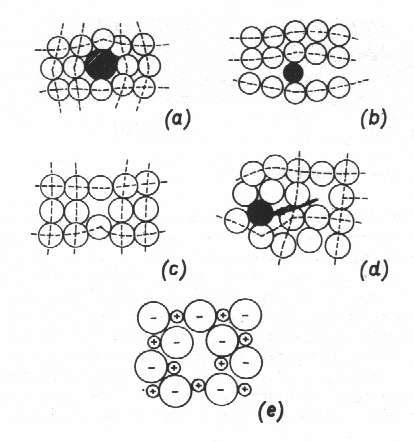Obr. 9.1 Typy bodových poruch: (a) substituční atom, (b) intersticiální atom, (c) vakance, (d) Frenkelova porucha.

   Dá se odvodit, že při každé nenulové teplotě musí existovat vakance, jejichž koncentrace je závislá na teplotě a na aktivační entalpii (energii) vzniku vakance. Při určitém zpracování krystalických látek však mohou vznikat vlastní bodové poruchy (vakance a intersticiály), jejichž koncentrace je vyšší než rovnovážná. Existují v podstatě tři metody, které zvyšují koncentraci vlastních bodových poruch nad hodnotu odpovídající rovnovážné koncentraci, a to zakalení z vysokých teplot, ozáření energetickými částicemi a plastická deformace.

   Zvýšíme-li teplotu krystalu na vysokou hodnotu velmi blízkou bodu tání, výrazně vzroste koncentrace bodových poruch, např. pro hliník při vysokých teplotách (asi 900 K) je koncentrace vakancí řádově 10^-4. Řádově stejné koncentrace bodových poruch bychom zjistili i pro jiné případy. Jestliže krystal budeme zchlazovat velmi pomalu, pak vakance (platí obecně i pro intersticiály, tudíž pro bodové poruchy) budou migrovat mříží do míst, kde se budou anihilovat (kde zaniknou). Jestliže však krystal prudce zchladíme na velmi nízkou teplotu (zakalíme), vakance nemohou dostihnout místa zániků a zůstanou v krystalu o koncentraci, která je mnohem větší než koncentrace odpovídající tepelné rovnováze při velmi nízké teplotě.

   Ozáření krystalu energetickými částicemi (neutrony, elektrony, alfa částicemi) způsobuje porušení vazeb mezi atomy. Atomy jsou nuceny (v důsledku srážek) opustit své pravidelné atomové polohy a zabudují se do intersticiálních poloh. Vznikají tak následkem ozáření vlastní bodové poruchy: vakance a intersticiály. Jejich koncentrace je opět mnohem vyšší (při dané teplotě) než rovnovážná koncentrace.

   Konečně při plastické deformaci se pohybují dislokace (druh čárové poruchy - viz další podkapitola). Pohybující se dislokace mohou protínat nepohyblivé dislokace. Vznikají tak stupně na dislokacích. Pohyb šroubových dislokací se stupni je však možný pouze za současného vzniku bodových poruch. To znamená, že v důsledku plastické deformace roste koncentrace bodových poruch na hodnoty vyšší než rovnovážná koncentrace.

     2.  Dislokace

   Dislokace jsou zvláštní druh poruch krystalové struktury. Než přejdeme k jejich definicím a popisu jejich vlastností, uveďme příklady dvou typů dislokací.

   Na obr. 9.2a je znázorněna hranová dislokace. Její vznik si můžeme představit tak, že krystal byl rozříznut podél roviny procházející shora dolů a do vzniklého řezu byla vložena polorovina. Podobnou situaci bychom obdrželi, kdybychom v dolní části krystalu jednu atomovou polorovinu odstranili. Okraj vložené poloroviny je čárová porucha.

   Šroubová dislokace je znázorněna na obr. 9.2b. Její vznik si můžeme představit tak, že krystal byl rozříznut v rovině, která je na obr. 9.2b vyšrafovaná až k přímce procházející bodem A kolmo na čelní stěnu. Horní část krystalu byla zasunuta dozadu o jednu meziatomovou vzdálenost a pak byl krystal opět spojen. Maximální porušení je podél přímky procházející bodem A, kolem dislokační čáry.

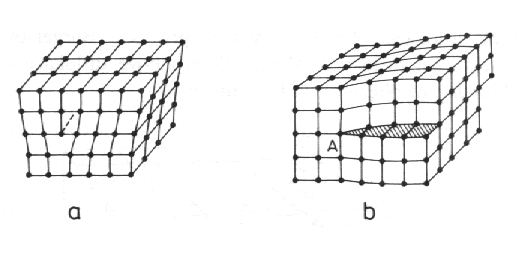Obr. 9.2 a) Hranová dislokace, b) šroubová dislokace.

   Dislokace je porušení krystalové struktury podél určité čáry, a proto se někdy označuje jako čárová porucha. Délka dislokace (dislokační čáry) může být rovna až rozměru krystalu.

   K přesné definici zavádíme soustavu tzv. t-vektorů, které mjí vlastnost, že a) spojují středy atomů se stejným okolím a b) nelze je nahradit kombinací vektorů kratších s vlastností a). Reálný krystal můžeme rozdělit na dvě oblasti: "dobrou oblast" ("neporušenou oblast") a "špatnou oblast" ("porušenou oblast"). Vektory t příslušející "dobrým oblastem" reálného krystalu, tj. takovým oblastem, jež nevykazují deformaci krystalové struktury, se neliší od příslušných vektorů t ideálního (dokonalého) krystalu. Určitému atomu ve "špatné" (porušené) oblasti, tj. v případě velkých deformací, nelze jednoznačně přiřadit "správné" nejbližší sousedy.

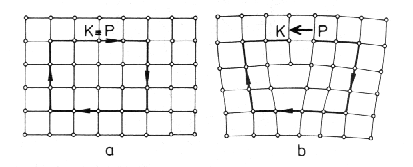Obr. 9.3 Burgersova smyčka ve struktuře s primitivní mříží v neporušené oblasti (a), a v porušené oblasti v případě hranové dislokace (b).

   Pod Burgersovou smyčkou budeme rozumět orientovanou křivku složenou z určitého počtu vektorů t. Vedeme Burgersovu smyčku v reálném krystalu v dobré oblasti tak, aby byla uzavřena. Přitom posloupnost vektorů t (jejich směr) může být libovolný (obr. 9.3a). Vedeme-li stejnou křivku v reálném krystalu špatnou oblastí (přičemž posloupnost vektorů t musí být stejná), pak je Burgesova smyčka neuzavřena. Vektor, kterým je nutno tuto smyčku uzavřít, tj. vektor spojující počáteční (P) a konečný bod (K) (obr. 9.3b), se nazývá Burgersův vektor b. Na obr. 9.3 je znázorněna hranová dislokace. Vidíme, že v případě hranové dislokace je Burgersův vektor b kolmý na dislokační čáru, která je přímá.

   Vznikne-li kolem čárové poruchy neuzavřená Burgersova smyčka, pak se tato porucha nazývá dislokace. V případě šroubové dislokace (obr. 9.4) je Burgersův vektor b rovnoběžný s dislokační čárou.

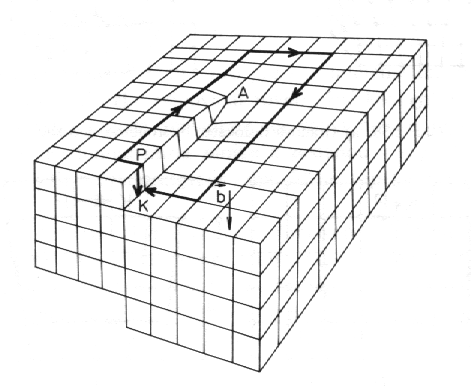Obr. 9.4 Burgersova smyčka (ve struktuře s primitivní mříží) v případě šroubové dislokace.

   Je zřejmé, že Burgersův vektor je podél dislokační čáry konstantní. Smysl Burgersova vektoru je určen směrem dislokační čáry s, tj. čáry vedené přibližně středem porušené oblasti, a smyslem oběhu Burgersovy smyčky. Pokud je Burgersův vektor dislokace translačním vektorem mříže, nazýváme tuto dislokaci úplnou. Burgersův vektor nabývá v každém typu krystalové mříže jen určitých hodnot. Tak v kubické plošně centrované mříži jsou nejkratší Burgersovy vektory typu b = 1/2 < 1 1 0 > o délce a / Ö2. Nejkratší Burgersovy vektory v kubické prostorově centrované mříži jsou typu b = 1/2 < 1 1 1 > o délce aÖ(2/3). V krystalech s kubickou primitivní mříží nejkratší Burgersovy vektory jsou typu b = < 1 0 0 > o délce a. Nejstabilnější dislokace v hexagonální struktuře s nejtěsnějším uspořádáním (směstnáním) mají Burgersův vektor typu b = 1/3 < 1 1 -2 0 > o délce a.

   Z definice dislokace (čárové poruchy) plyne, že dislokační čára musí být buď uzavřená (dislokační smyčka) nebo začínat a končit na povrchu krystalu nebo začínat (končit) na povrchu a končit (začínat) na jiné dislokaci. Znovu zdůrazňujeme, že Burgersův vektor je konstantní podél celé dislokační čáry. Mění se pouze orientace dislokační čáry, a tudíž i vzájemná poloha Burgersova vektoru b a elementu dislokační čáry s. Dislokace je tak charakterizována dislokační čárou a Burgersovým vektorem.

   V reálném krystalu neexistuje pouze jedna dislokace. Pozorujeme dislokační strukturu. Jako charakteristika dislokační struktury se zavádí hustota dislokací r_D udávající délku dislokačních čar v jednotce objemu. Hustota dislokací je tudíž definována vztahem

kde Sl je celková délka dislokačních čar v objemu V. Tudíž její rozměr je m^-2. Hustotu dislokací je možno určit jako počet průsečíků dislokačních čar s povrchem v jednotkové ploše. Hustota dislokací může podstatně ovlivnit fyzikální vlastnosti krystalických materiálů. Tak u kovových krystalů hustota dislokací roste s rostoucí deformací. Příprava kvalitních polovodičových součástek vyžaduje takový způsob, aby hustota dislokací byla co nejnižší.

   Hustota dislokací udává však jen základní představu o dislokacích. Dislokační struktura je charakterizována velikostí a směrovým rozdělením Burgersových vektorů, tvarem a uspořádaním dislokačních čar. Na obr. 9.5 je ukázka dislokační struktury získané transmisní elektronovou mikroskopií.

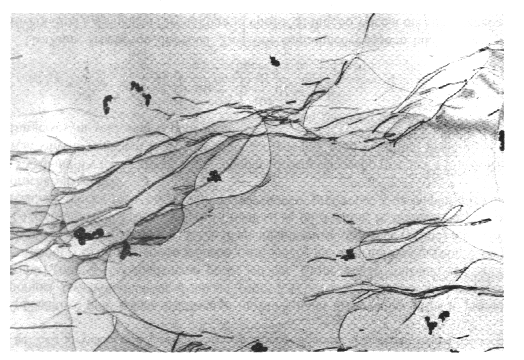Obr. 9.5 Dislokační struktura získaná transmisní elektrovou mikroskopií.

     3.  Plošné a objemové poruchy

   Plošné poruchy. Změna koordinace atomů celé roviny může vzniknout poruchou v pravidelnosti vrstvení rovin během krystalizace. Na obr. 6.6 je znázorněna struktura vzniklá vrstvením těsně uspořádaných rovin. Sled rovin můžeme označit typem vrstvení ... ABC ABC ABC ... a vzniklá struktura nejtěsněji směstnaných koulí má symetrii kubické plošně centrované mříže. Dojde-li při vrstvení k poruše, např. tak, že se vytvoří sled ... ABC AB ABC ABC ... , vznikne v porušené oblasti vrstva s těsně uspořádanou strukturou typu ... AB AB ... a ta má symetrii hexagonální mříže (obr. 6.5). Změna v pravidelnosti vrstvení atomových rovin se nazývá vrstevná porucha.

   Nejběžnějším typem plošných poruch jsou hranice vznikající při růstu krystalu mezi jednotlivými zrny. Tzv. vysokoúhlové hranice vzniknou v obecném případě, když se setkají dvě zrna rostoucí z různých zárodků. Pojmenování tohoto typu hranic je dáno obecně velkými úhly vzájemné orientace mříží sousedních zrn. Speciálním případem vysokoúhlových hranic je rozhraní mezi zrcadlovými protějšky u dvojčat (obr. 9.6).

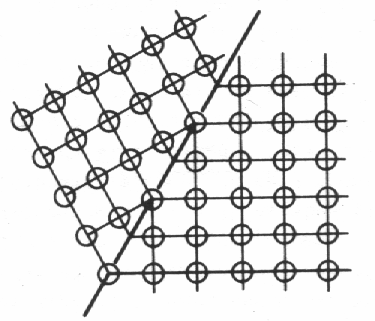Obr. 9.6 Dvojčatová hranice.

   I v poměrně dokonalých krystalech se může vyskytovat další typ hranic - nízkoúhlové. Tyto hranice jsou tvořeny dislokacemi, uspořádanými rovnoběžně podél určitých rovin (obr. 9.7). Úhlová separace sousedních, relativně dokonalých krystalových oblastí je řádově rovna úhlovým minutám.

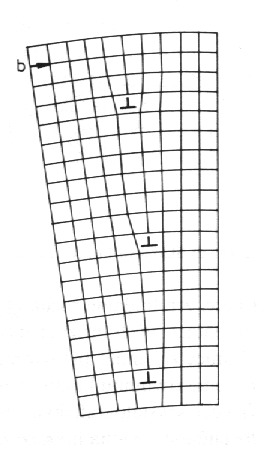Obr. 9.7 Symetrická sklonová maloúhlová hranice.

   Objemové poruchy. Stejně jako se u dislokací projevuje tendence ke shlukovámí podél rovin, tak také bodové poruchy mají tendenci ke shlukování. Vakance se mohou např. shlukovat a vytvářet větší dutiny v krystalech, které se mohou dále rozpadnout na dislokace nebo tvořit trhliny. Intersticiální atomy se mohou shlukovat a vytvářet precipitáty různých tvarů, např. shlukováním podél určitých rovin vznikají dvojrozměrné precipitáty. Nebo substituční atomy se mohou kombinovat s hostitelskými atomy a vytvářet uspořádané sledy, lišící se od struktury hostitelského krystalu. Tyto jevy vedou k vylučování (segregaci) samostatných fází.