III. PROSTOROVÉ MŘÍŽE A KRYSTALOVÉ SOUSTAVY
1. Rovinné mříže*, operace
symetrie*
Prvek symetrie přítomný v krystalu musí vyhovovat symetrickému uspořádání mřížových bodů, které je dáno translační periodicitou mříže a naopak prvek symetrie krystalu určuje, jaký druh mříže může tento krystal mít. Má-li být například prvkem symetrie rotační osa, musí být mříž symetrická vůči otáčení kolem nějaké osy A o úhel a a jeho celistvé násobky. Kdybychom tuto operaci prováděli opakovaně, pak se mříž po n otočeních dostane do výchozí polohy, neboli platí
|
|
(3.1) |
Takovouto rotační osu pak nazýváme rotační n-četná osa nebo jen n-četná osa (např. dvojčetná, trojčetná apod.) a v mezinárodní symbolice ji označujeme číslicí n (tj. 1, 2, 3 atd.). Jednočetná osa se nazývá identita. Naskýtá se otázka, jakých četností mohou rotační osy nabývat u trojrozměrně periodických vzorů, tj. i u ideálních krystalů. Již rovinné mříže určují tato omezení četnosti rotačních os, neboť prostorové mříže vznikají z rovinných jejich vrstvením.
|
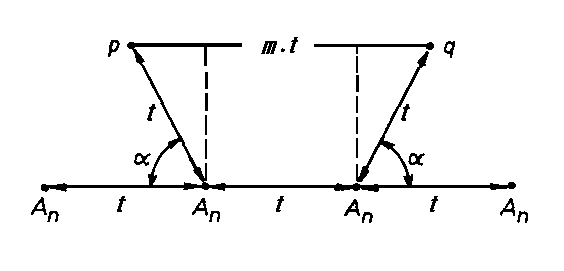
| Obr. 3.1. |
Ve spodní části obr. 3.1 je znázorněna řada mřížových bodů nějaké rovinné mříže, vzdálených o délku t translační periody. Uvažujme obecnou n-četnou osu An umístěnou v každém mřížovém bodě kolmo k nákresně. Osy An procházející dvěma prostředními mřížovými body opakují translace t po a stupních (a=2p/n) na obě strany. Má-li být rovinná mříž symetrická vůči těmto osám An, musí se mřížové body vyskytovat i na koncích pootočených translací t. Mřížové body p a q, které takto vzniknou, jsou stejně vzdáleny od základní mřížové řady a leží v nelbližší řadě mřížových bodů. Translační periodita rovinné mříže však vyžaduje, aby jejich vzdálenost byla celistvým násobkem periody t. Možné hodnoty úhlu a lze tak určit z geometrické podmínky
|
mt = t + 2tcos a, m = 0, ±1, ±2, ±3, ...., cos a = (m-1)/2. |
(3.2) |
Jelikož hodnota |cos a| může být pouze menší nebo rovna jedné, dostáváme pro
m-1 od -2
do +2 pět hodnot dovolených úhlů a, a tudíž i pět dovolených četností rotačních os
konzistentních s translační periodicitou mříže (tab 3.1).
m - 1
cos a
a ( ° )
n
-2
-1
0
+1
+2-1
-1/2
0
+1/2
+1180
120
90
60
0 nebo 3602
3
4
6
1
Z uvedeného je patrné, že pětičetná
osa a osy s četností větší než 6 nejsou slučitelné s translační periodicitou mříže. Je však
třeba poznamenat, že i tyto "zakázané" osy se mohou v krystalech vyskytovat jako prvky
symetrie celé struktury ideálních krystalů. Rovněž tak se mohou vyskytovat u přírodních
objektů, jako jsou např. květiny, u kterých odpadá omezení dané u krystalů jejich translační
periodicitou.
|
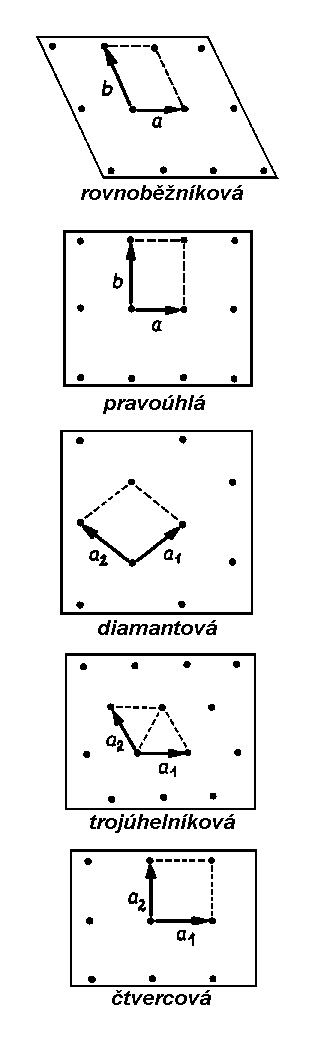
| Obr. 3.2 Rovinné mříže.* |
Trojrozměrné mříže bychom nyní mohli vytvářet vrstvením rovinných mříží nad sebou. To je možné provést více způsoby. Nežli k tomu přistoupíme, povšimněme si nejprve rozložení os otáčení v rovinných mřížích. Je-li kombinována rotační osa s kolmou translací, musí existovat i rotační osa rovnoběžná s výchozí. To znamená, že např. rovnoběžníková rovinná mříž, konzistentní s 2četnými osami umístěnými v mřížových bodech, je konzistentní ještě s dalšími 2četnými osami lokalizovanými mimo mřížové body v důsledku kombinace původních os s translacemi mříže. Rozmístění těchto os pochopíme snadno, obklopíme-li translačně ekvivalentní 2četné osy, tj. osy umístěné v mřížových bodech, asymetrickým motivem (obr. 3.3). Je patrné, že musí existovat i 2četné osy umístěné uprostřed mezi translačně ekvivalentními osami.
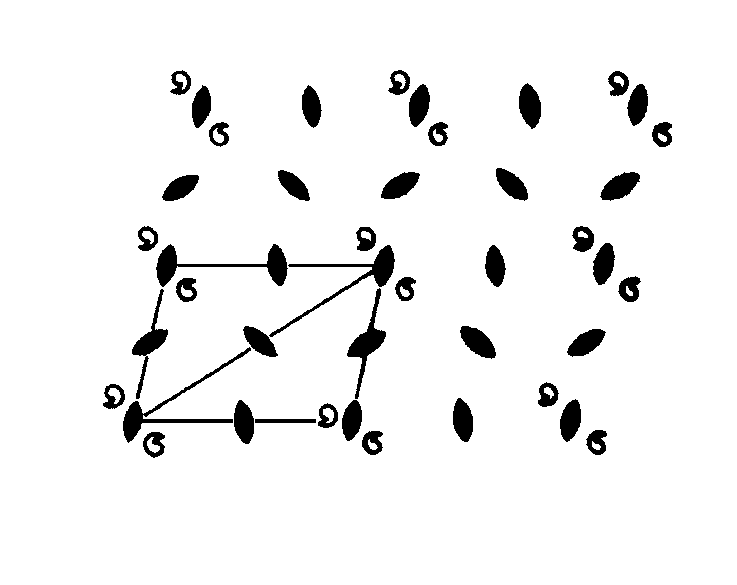
|
| Obr. 3.3. |
Podobně bychom mohli postupovat i u ostatních rovinných mříží. Kombinace prvků symetrie s translacemi rovinných mříží se nazývají rovinné grupy a existuje 17 typů rozdílných rovinných grup. Tři z nich jsou znázorněny na obr. 3.4 a z něj je patrno, že nově vzniklé rotační osy mohou mít i jinou četnost než původní (o tom se lze opět přesvědčit pomocí opakovaných motivů).
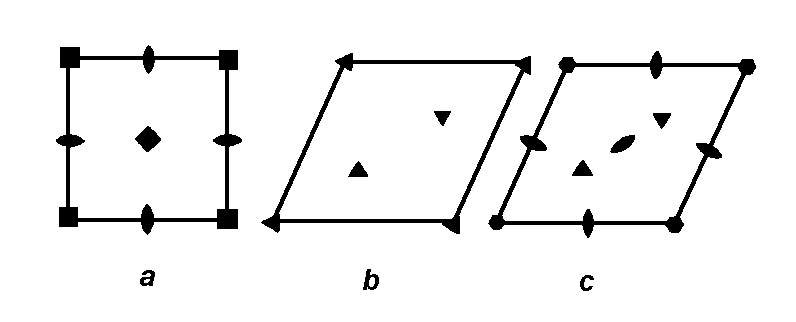
|
| Obr. 3.4. |
2. Prostorové mříže*
Trojrozměrné mříže si můžeme představit jako sled rovinných mříží vzniklý periodickým opakováním těchto rovinných mříží translací ve třetím rozměru. V případě rovnoběžníkové mříže, konzistentní s 1, můžeme další rovinnou mříž umístit nad výchozí do libovolné polohy a získáme tak nejobecnější prostorovou mříž. Její primitivní buňka je rovnoběžnostěn s nestejnými délkami hran a s nestejnými úhly mezi nimi.
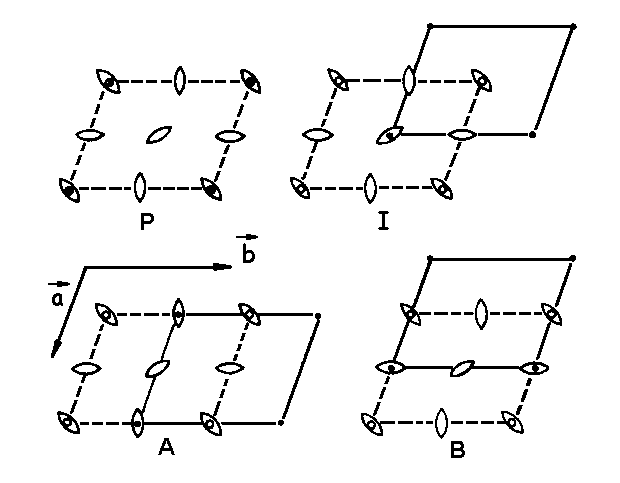
Při vrstvení mřížových rovin konzistentních s 2 máme čtyři možnosti, jelikož rovnoběžníková rovinná mříž má čtyři translačně neekvivalentní skupiny 2četných os (ekvivalentní 2četné osy jsou na obr. 3.3 znázorněny stejně skloněnými symboly). Tyto čtyři možnosti vrstvení jsou znázorněny na obr. 3.5, kde kroužky a tečky v místech mřížových bodů označují výchozí a následnou mřížovou rovinu. Z obrázku je zřejmé, vrstvení P dává primitivní buňku, vrstvení I buňku neprimitivní s mřížovým bodem ve středu tělesové úhlopříčky a vrstvení A a B neprimitivní buňku s mřížovými body ve středech bočních stěn. Dá se však ukázat, že případy A a B jsou totožné s případem I, zvolíme-li úhlopříčku rovnoběžníka za jednu hranu buňky. Existují tedy pouze dva rozdílné typy prostorových mříží vzniklých vrstvením rovnoběžníkových rovinných mříží konzistentních s 2. Přítomnost 2četné osy v obou těchto mřížích vyžaduje, aby hrana buňky rovnoběžná s touto osou byla současně kolmá ke zbývajícím dvěma hranám: elementární buňka má tedy parametry aąbąc, a=b= 90°ąg. Volba krystalografické osy rovnoběžné s dvojčetnou osou a volba zbývajících dvou os tak určují typ centrování u centrované mříže (viz tab. 3.2 a obr. 3.5).
| Symbol | Typ centrování | Souřadnice mřížových bodů v buňce |
|---|---|---|
| P | primitivní | 0, 0, 0 |
| C | bazálně centrovaná | 0, 0, 0; 1/2, 1/2, 0 |
| A | bazálně centrovaná | 0, 0, 0; 0, 1/2, 1/2 |
| B | bazálně centrovaná | 0, 0, 0; 1/2, 0, 1/2 |
| I | prostorově centrovaná | 0, 0, 0; 1/2, 1/2, 1/2 |
| F | plošně centrovaná | 0, 0, 0; 1/2, 1/2, 0; 0, 1/2, 1/2; 1/2, 0, 1/2 |
| R | romboedricky centrovaná vzhledem k hexagonálním osám |
0, 0, 0; 2/3, 1/3, 1/3; 1/3, 2/3, 2/3 |
primitivní vzhledem k romboedrickým osám | 0, 0, 0 |
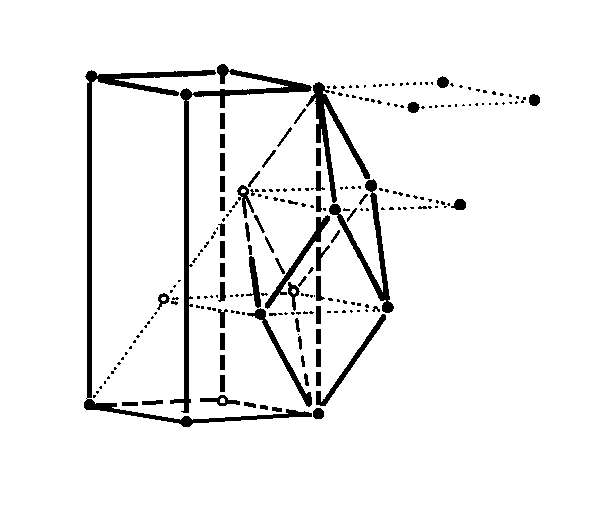
Kombinace os 4, 3 a 6 s kolmými translacemi čtvercové a trojúhelníkové mříže má za následek vznik dalších os. Jejich umístění v základních buňkách rovinných mříží je uvedeno na obr. 3.4. Při vrstvení rovinných mříží obsahujících pouze trojčetné osy vznikají dva typy prostorových mříží. Jedna vznikne kolmou translací rovinné mříže a je primitivní. Druhý typ mříže je znázorněn na obr.3.6. V této mříži lze zvolit dvě různé buňky: primitivní buňku ve tvaru romboedru (klence) nebo centrovanou buňku ve tvaru kolmého rovnoběžnostěnu s centrujícími body v 1/3 a 2/3 tělesové úhlopříčky. Trigonální krystaly * s tímto typem mříže lze tedy popsat buď pomocí romboedrických os (a=b=c, a=b=gą90°), a nebo pomocí hexagonálních os (a=bąc, a=b=90°, g=120°).
|
| Obr. 3.6. |
3. Krystalové soustavy
Soubor prvků symetrie krystalu se nazývá bodová grupa * a prostorová mříž krystalu musí být v souladu s jeho bodovou grupou. Dá se ukázat, že existují určité prvky symetrie společné vždy pro určitou skupinu bodových grup, což vede k přirozenému rozdělení krystalů do krystalových soustav podle těchto společných prvků symetrie. Krystalové soustavy byly vzhledem ke své užitečnosti pojmenovány. Jsou uvedeny v tabulce 3.3 (názvosloví není zcela jednotné, v závorce jsou uvedeny ekvivalenty) spolu se společnými minimálními prvky symetrie, což jsou minimální symetrie postačující k zařazení krystalu do dané krystalové soustavy - jsou diagnostickými prvky každé soustavy.
| krystalová soustava | minimální symetrie |
|---|---|
| triklinická (trojklonná) | žádná |
| monoklinická (jednoklonná) | jedna 2četná osa podél c |
| ortorombická (rombická, kosočtverečná) | tři 2četné osy podél a, b , c |
| tetragonální (čtverečná) | jedna 4četná osa podél c |
| kubická (izometrická) | čtyři 3četné osy podél tělesových úhlopříček krychle |
| hexagonální (šesterečná) | jedna 6četná osa podél c |
| trigonální (romboedrická, klencová) | jedna 3četná osa podél hexagon. buňky |
4. Bravaisovy mříže
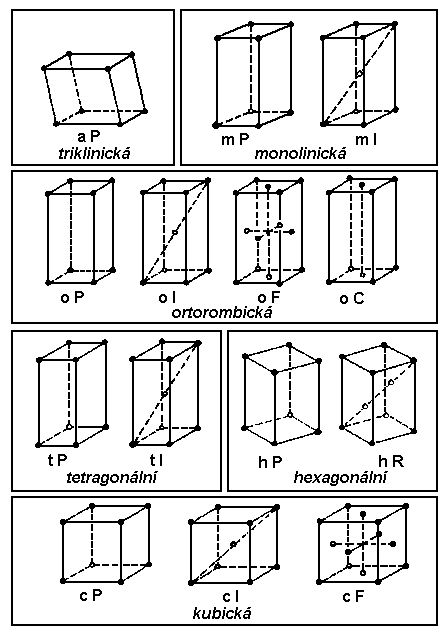
Dá se dokázat (např. systematickým vyšetřováním možných způsobů vrstvení rovinných mříží), že existuje pouze 14 různých prostorových mříží. Nazývají se také Bravaisovy mříže podle autora prvního úplného odvození (r. 1850). Jejich rozdělení do krystalových soustav je uvedeno v tab. 3.4 a grafické znázornění je na obr. 3.7.
|
| Obr. 3.7 Konvenční buňky 14 prostorových mříží. (U monoklinické soustavy je zde význačná osa c kolmá k základně buňky. Existují však i jiné volby centrované buňky v mřížích mI a oC - viz tab. 3.4. Hexagonální krystaly mají pouze primitivní mříž hP. Některé trigonální krystaly mají mříž hP, jiné mříž hR, a tudíž často užívaná základní buňka trigonální soustavy ve tvaru romboedru - klence nevystihuje mříž všech trigonálních krystalů.). |
V tab. 3.4 a na obr. 3.7 jsou prostorové mříže rozděleny do šesti krystalových rodin v důsledku přiřazení mříží konzistentních s 3 k hexagonální soustavě, i když by podle symetrie příslušely k soustavě trigonální. Důvod tohoto přiřazení spočívá v tom, že při klasifikaci mříží je rozhodující typ mříže spíše než minimální symetrie. Daným přiřazením se dosáhne jednotnosti popisu mříží konzistentních s 3 pomocí jediného systému os (viz znovu obr. 3.6).
| Krystalová rodina | Symbol | Krystalová soustava |
Konvenční soustava souřadnic | Bravaisovy mříže | |
| omezení parametrů mříže | určované parametry |
||||
| triklinická | a | triklinická | žádné | a, b, c a, b, g | aP |
| monoklinická | m | monoklinická | význačná osa b a = g = 90° |
a, b, c b | mP mC (mA, mI) |
| význačná osa c a = b = 90° |
a, b, c g | mP mA (mB, mI) |
|||
| ortorombická | o | ortorombická | a = b = g = 90° | a, b, c | oP oC (oA, oB) oI oF |
| tetragonální | t | tetragonální | a = b a = b = g = 90° |
a, c | tP tI |
| hexagonální | h | trigonální | a = b a = b = 90° g = 120° (hexagonální osy) |
a, c | hP |
| a = b = c a = b = g (romboedrické osy) |
a, a | hR | |||
| hexagonální | a = b a = b = 90° g = 120° |
a, c | hP | ||
| kubická | c | kubická | a = b = c a = b = g = 90° |
a | cP cI cF |