Grupa

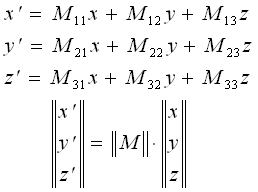
Množina G s prvky a, b, ..., mezi nimiž je definováno násobení, je grupou, pokud platí následující tvrzení:

• pro každá a a b z G je ab prvkem G,
• pro každá a, b, c z G je (ab) c = a (bc) - asociativní zákon
• v G existuje jednotkový prvek e, pro který je ae = ea = a, pro každé a z G (identita)
• ke každému a z G existuje inverzní prvek a^-1, pro který je aa^-1 = a^-1a = e (inverze)

Řád grupy
počet prvků

Příklady grup: celá čísla, racionální čísla bez nuly, sada polohových vektorů mříže (e = r(0,0,0))

Prvky krystalografických grup - operace symetrie

Abelovská grupa

platí také komutativní zákon

Cyklická grupa

G₁ = (g, g², ..., g^n-1, gⁿ =e)

jakákoli grupa může být výjadřena pomocí součinu mocnin maximálně tří prvků - generátory grupy
(např. 6/m - 6_[001], -2_[001])

Multiplikační tabulka

Každý prvek se v jedné řádce objevuje právě jednou.

Izomorfní grupy

Mají stejné multiplikační tabulky, stejný řád. Jsou generovány ze stejné abstraktní grupy.

Př.  222 {1, 2, 2, 2}, 2/m {1, 2, m, -1}, mm2 {1, m, m, 2}

Podgrupy (subgroup)

část grupy, která je sama grupou. Příklady: sudá čísla jsou podgrupou celých čísel.

grupa 32 {g₁ = 1, g₂ = 3_[001], g₃ = 3² = 3^-1, g₄ = 2_[100], g₅ = 2_[010], g₆ = 2_[-1-10], podgrupa H = {g₁, g₂, g₃}
grupa 422, podgrupa 222

Nadgrupy (supergroup)

Důležité pro studia fázových transformací a studium přechodů pořádek-nepořádek.

(coset)

Nechť H = (h₁, h₂, ...) je podgrupa G, g_i prvek G, který není v H. Potom součiny

g_iH = (g_ih₁, g_ih₂, ...) a Hg_i tvoří levý a pravý coset H. H s nimi nemůže mít  žádný společný prvek .

Grupa G může být rozložena vzhledem k H

G = H U g_iH U g_qH U ...

např. 2/m = 1(1, 2) U -1(1, 2) = (1, 2) U (-1, m)

Počet různých coset získaných z dekompozice grupy vzhledem k podgrupě ze nazývá index podgrupy.

Konjugované třídy

Prvek g_i se nazývá konjugovaný k prvku g_j z G, pokud G obsahuje prvek g_k, že g_i =( g_k)^-1g_jg_k. Pro fixní g_j tvoří g_i třídu konjugovaných prvků.

g_k - transformace souřadnic operátorem symetrie, g_j - maticový operátor vztažený k jiné operaci symetrie.
Operátory symetrie stejné třídy jsou vztaženy transformací souřadnic pomocí prvku grupy.

př. 32: tři třídy - (e), (3, 3^-1), (2_[100], 2_[010], 2_[-1-10])

Třídy bodových grup:

1. jsou tvořeny pouze jedním prvkem až do ortorombické (tzn. všechny operátory symetrie jsou navzájem komutativní)
2. v abelovských grupách jsou třídy tvořeny jedním prvkem
3. operátory identity, inverze a zrcadlení kolmo k hlavní ose symetrie jsou všechny ve zvláštních třídách

Konjugované podgrupy

Nechť H je podgrupa G a g je prvkem G, který není v H. Potom všechny prvky g^-1Hg tvoří grupu. H a g^-1Hg jsou konjugované grupy.

Normální podgrupy (invarianty)

Podgrupy, které jsou transformované samy na sebe aplikací všech prvků grupy.

př. 32:  - (1, 3, 3^-1) normální , (1, 2_[100]) není normální.

Nechť H je normální podgrupa G s indexem p a n je řád G.
Řád H je n/p. 
(g_iHg_jH) = g_iHHg_j = g_iHg_j = g_ig_jH, (g_iH)^-1(g_iH) = H^-1(g_i)^-1g_iH = e
H(g_iH) = g_iHH = g_iH

Faktorová grupa 

G/H  s prvky cosets H

Homomorfismus 

G -> G/H (korespondence n/p -> 1 resp. více -> 1)

Izomorfismus 

Příklad:

G = 23

G = {1, 3_[111], 3²_[111], 3_[-111], 3²_[-111], 3_[1-11], 3²_[1-11], 3_[11-1], 3²_[11-1], 2_[100], 2_[010], 2_[001]}

4 třídy: (1), (3_[111], 3_[-111], 3_[1-11], 3_[11-1]), (3²_[111], 3²_[-111], 3²_[1-11], 3²_[11-1]), (2_[100], 2_[010], 2_[001])

10 podgrup: {1}, {1, 2_[100]}, {1, 2_[010]}, {1, 2_[001]}, {1, 3_[111], 3²_[111]}, {1, 3_[-111], 3²_[-111]}, {1, 3_[1-11], 3²_[1-11]}, {1, 2_[100], 2_[010], 2_[001]}

Invariantní: {1}, {1, 2_[100], 2_[010], 2_[001]} a G

Faktorová grupa podgrupy H = {1, 2_[100], 2_[010], 2_[001]} 
-> např. 3_[111]H = {3_[111], 3_[-111], 3_[1-11], 3_[11-1]}, 3²_[111]H = {3²_[111], 3²_[-111], 3²_[1-11]} 3²_[11-1]

G = H U 3_[111]H  U 3²_[111]H

g1 = e
{e,  3_[111]H, 3²_[111]H} tvoří grupu s následující multiplikační tabulkou

Vlastní podgrupa

Podgrupa H je nazývána vlastní podgrupa grupy G, pokud existují operace symetrie, které jsou obsaženy v G a nejsou obsaženy v H.

Maximální podgrupa

Podgrupa H grupy G je nazývána maximální podgrupou G, jestliže neexistuje vlastní podgrupa M grupy G taková, že H je vlastní podgrupou M.

Minimální nadgrupa

G´ se nazývá minimální nadgrupa grupy G, jestliže G je maximální podgrupa G´.

Dekompozice-
eliminace některých prvků symetrie - t-podgrupy (Translationengleiche) - maximální neizomorfní podgrupy typu I
ztráta translační symetrie - k-podgrupy (Klassengleiche) - typ II (maximální izomorfní podgrupy)

Krystalografické transformace -

 působení operací symetrie na prvky krystalografických grup

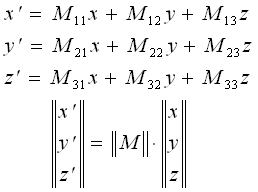
Identita (1)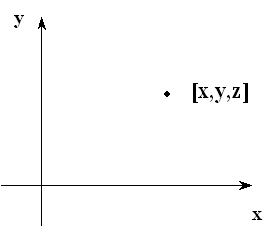
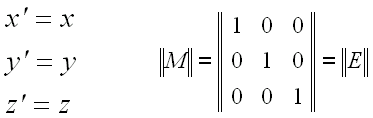Inverze (-1)
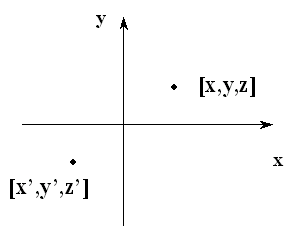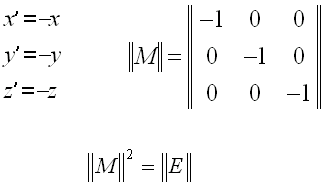Zrcadlení (m)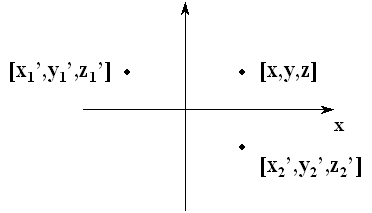
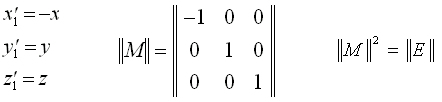
Rotace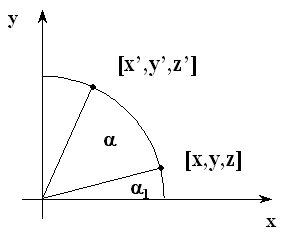

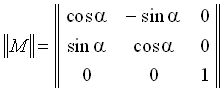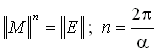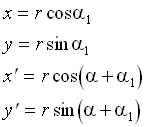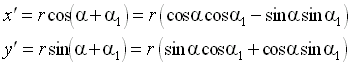
Kombinace 2 || z  a  m (xz):

2 = {R₂(z), E} 
m = {M(x, z), E} -->   

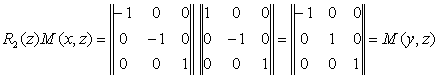       Bodová grupa C_2v = mm2,   {E, R₂(z), M(x, z), M(y, z)}

Multiplikační tabulka