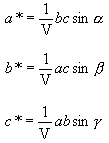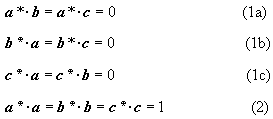
Let (O, a, b, c) be our coordinate system (in a crystal, a,b,c are usually the elementary translations of the space lattice). A second coordinate system may be introduced (O, a*, b*, c*), reciprocal to the first one, defined by the following conditions:

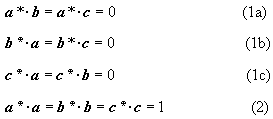
The conditions (1a), (1b), (1c) suggest that a*, b*, c* are normal to the planes (b, c), (a, c), (a, b) respectively. The modulus and sense of a*, b*, c* are fixed by the conditions (2). If a* is normal to the plane (b, c) then it may be written as:

where p is a constant to define. The value of p is obtained by multiplying the right and left side of (3) by a.

from which p = 1/V.

The equation (3) and its analogue may be written as:

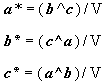
or in terms of moduli: