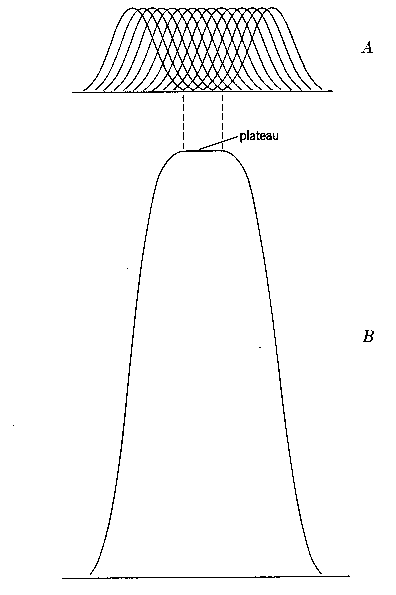
Obr. 1
Laueho
metoda- Ewaldova konstrukce. Podle Amoróse, Buergera a Amoróse [2].
Jiří Hybler
Fyzikální
ústav AVČR, Cukrovarnická 10, 162 53 Praha
6
Před nástupem
difraktometrů představoval fotografický film jediné vhodné medium
pro registraci paprsků difraktovaných na monokrystalech. Proto bylo
vyvinuto několik důmyslných metod pro snímání difrakčních
obrazců, z nichž některé dosáhly značného rozšíření a
příslušné komůrky byly komerčně produkovány. Pokrok v
difraktometrii způsobil, že tyto metody byly postupně zatlačeny
do pozadí. Zejména ztratily význam pro měření intenzit, pro které
byly těžkopádné a nepřesné. Jsou stále používány pro určení
mřížkových parametrů, ale s přesností o jeden až dva řády
horší, než u difraktometru. Nicméně jako pomocné metody si svůj význam
stále podržují, zejména díky možnosti zobrazit určitou oblast
(zpravidla řez) reciprokého prostoru „se vším všudy”, to jest například
s difuzními pásy, satelitními difrakcemi, difrakčními stopami dvojčat
nebo epitaxních srostlic více fází. Získání odpovídající informaci
pomocí difraktometru s bodovým detektorem je velmi obtížné a pro větší
oblast reciprokého prostoru prakticky - z časových důvodů -
nemožné, pomocí difraktometru s plošně citlivým detektorem sice
principielně možné, ale ne vždy podporované softwarově. Užitečnost
filmových metod se proto ukazuje tehdy, když při měření na
difraktometru nastanou nečekané potíže. Filmové metody rovněž umožňují
posoudit kvalitu krystalu a jeho vhodnost pro další měření. Z tohoto
důvodu si tyto metody stále zaslouží přiměřenou
pozornost.
Sluší
se podotknout, že technický pokrok se dotkl i těchto do značné míry
překonaných metod. Je možné digitalizovat filmový obraz
pomocí scaneru a dále jej zpracovávat v počítači. Další
možností je registrace difrakčního obrazu na speciální folii, obdobnou
tzv. image plate, která je umístěna do kazety místo běžného
filmu. Latentní obraz z folie lze pomocí speciální, ale bohužel nákladné
čtečky přenést přímo do počítače a posléze jej
vymazat pro opětné použití folie. Folie a čtečky dodává např.
firma Fuji nebo Molecular Dynamics.
V dalším
textu bude pro zjednodušení použit nadále pojem „film” v nejširším
slova smyslu, to jest jak pro klasický film, tak pro speciální registrační
folie.
Připomeňme
si některé základní skutečnosti:
Každý
difrakční obraz je obrazem určité části reciproké mříže
nebo obecněji reciprokého prostoru. Jednotlivé metody se liší tím,
jakou část reciprokého prostoru zobrazují. Obraz reciproké mříže
(prostoru) může být navíc ještě zkreslený, a/nebo zkolabovaný.
Protože reciproký prostor je trojrozměrný a registrační medium -
film pouze dvojrozměrný, je principielně možné zobrazit
nezkolabovaně pouze dvojrozměrný řez reciprokou mříží
(prostorem). Obraz nějakého trojrozměrného výseku reciprokého
prostoru na dvojrozměrném filmu proto musí být nutně zkolabovaný.
Nutnou podmínkou pro vznik nezkresleného obrazu reciproké mříže je
shodnost pohybu krystalu a filmu. Pokud je jejich pohyb rozdílný, popřípadě
pokud film stojí, je obraz reciproké mříže zkreslen. Poznamenejme, že
skutečně nezkreslený a nezkolabovaný trojrozměrný obraz
reciprokého prostoru lze v některých případech získat ve formě
bitmapy z difraktometrických dat z pozičně citlivého
detektoru.
Tento
text si klade za cíl seznámit čtenáře se základy filmových metod
a některými příklady použití z autorovy praxe. Zájemce o důkladnější
studium odkazuji např. na podrobný text Helliwela [1] a
na monografie týkající se jednotlivých metod, citované v příslušných
kapitolách.
Tato metoda je historicky nejstarší a byla nazvána po objeviteli
rentgenové difrakce. Jejímu podrobnému popisu je věnována monografie
Amoróse, Buergera a Amoróse [2].
 |
|
Obr. 1 |
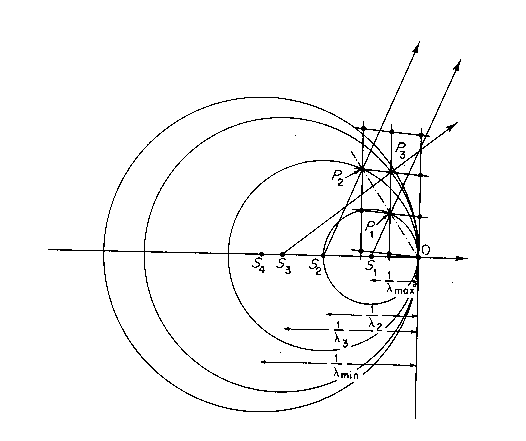
Princip metody je následující: paprsek nefiltrovaného a proto polychromatického záření dopadá na stacionární krystal. Při dané mezirovinné vzdálenosti a fixovaném krystalu se difrakce zúčastňuje ta vlnová délka, pro kterou je splněna Braggova podmínka. Ewaldova konstrukce je na obr. 1. Namísto jediné Ewaldovy koule máme jakési kontinuum Ewaldových koulí odpovídajících všem vlnovým délkám obsažených v záření. Na schématu jsou znázorněny ty z nich, pro které je splněna Braggova podmínka pro některý uzel zobrazeného kousku reciproké mříže. Jejich poloměry jsou 1/λ2, 1/λ3 a dotýkají se ve společném bodě O, počátku reciproké mříže. Ewaldovy koule o poloměrech 1/λmin a 1/λmax odpovídají minimální a maximální vlnové délce obsažené ve spektru a vymezují oblast reciprokého prostoru přístupnou difrakci. Všimněme si že středy Ewaldových koulí nejsou totožné, ale leží na společné přímce. Všimněme si dále, že difraktované paprsky z uzlů hkl a 2h2k2l – na nákresu označených jako P1 a P2 - míří stejným směrem a proto dají vznik stejné difrakční stopě na snímku. Z toho mj. vyplývá, že difrakční stopa na lauegramu může být tvořena superpozicí stop více řádů. Obraz reciproké mříže je zkolabovaný do radiusvektorů bodů reciproké mříže a zkreslený projekcí na plošný (popř. válcový) film.
|
|
|
Obr. 2 |
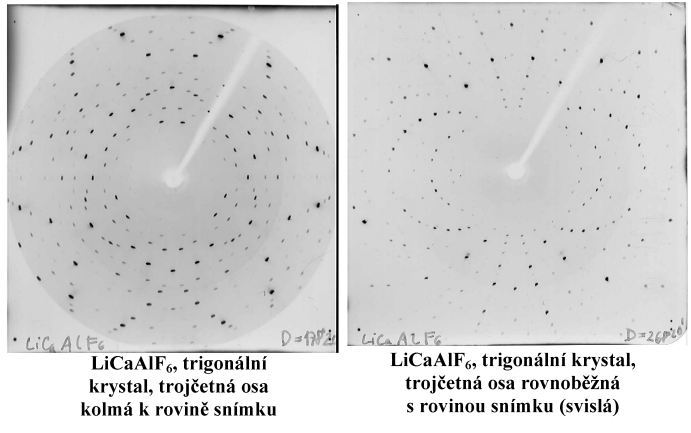
V praxi se nejběžněji používá uspořádání s plošným filmem kolmým k primárnímu paprsku umístěný buď na průchod, nebo na odraz (obr. 2). V prvním případě dopadají difraktované paprsky na plošný film, umístěný v kazetě za krystalem. Ukázka snímků na průchod je na obr. 3. V druhém případě je kazeta umístěna mezi rentgenkou a vzorkem, přičemž kolimátor vymezující primární svazek prochází otvorem v kazetě. Uspořádání na průchod vyžaduje dostatečně malý krystal, a proto je používáno poměrně zřídka. Naopak uspořádání na odraz neklade žádná omezení na velikost krystalu a proto je používána pro orientaci velkých monokrystalů - viz dále. V takovém případě se ovšem difrakce účastní jenom malá část krystalu v místě dopadu paprsku.
 |
|
Obr. 3 |
Rovinám reciproké mříže (a tedy příslušným pásmům
rovin v přímé mříži) odpovídají difraktované paprsky ležící
na plochách Laueho kuželů. Jeden z těchto kuželů je znázorněn
na obrázku 2. Na snímcích se roviny reciproké mříže jeví jako
girlandy difrakčních stop ve tvaru kuželoseček – elips na snímcích
na průchod a hyperbol na snímcích na odraz. Ve specielním případě,
kdy je rovina reciproké mříže rovnoběžná s primárním paprskem
(a tedy kolmá k rovině filmu) degeneruje Laueho kužel na rovinnou plochu,
jejíž projekcí je girlanda ve tvaru přímky. Difrakční stopy odpovídající
význačným bodům reciproké mříže nacházíme v průsečících
girland a tyto stopy se jeví jako poněkud izolované od ostatních.
Intenzita difrakčních stop odvisí jednak od strukturního faktoru
difraktujících mřížkových rovin, jednak od vlnové délky záření.
Pokud je Braggova podmínka náhodou splněna pro charakteristickou čáru,
jeví se taková difrakční stopa - popřípadě pouze její část
- jako abnormálně silná.
|
|
|
Obr. 4 |
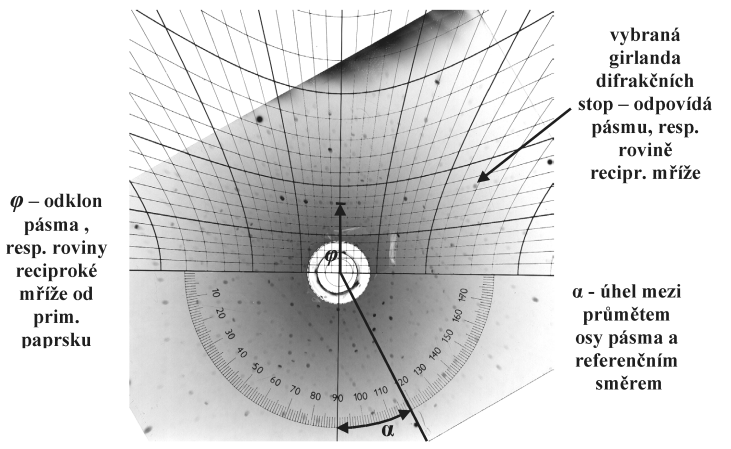
Pro interpretaci lauegramů se používají specielní sítě – Dunnova pro snímky na průchod a Greningerova pro snímky na odraz (obr. 4). Vzhledem k praktickému využití popíši použití Greningerovy sítě.
Greningerovu síť tvoří dva systémy hyperbol. Podle pravolevých
hyperbol určujeme odklon osy pásma (přímého vektoru) od roviny
filmu, respektive odklon roviny reciproké mříže od primárního paprsku.
Pro normalizovanou vzdálenost vzorek – film 30 mm odpovídá rozteč
hyperbol úhlovému rozdílu 2°. Každá pátá hyperbola je vyznačena tučně a odpovídá úhlovému
rozdílu 10°. Vybranou girlandu ztotožníme s pravolevou hyperbolu (obr. 5) Pořadí
hyperboly nám určí úhlovou odchylku odpovídající roviny reciproké mříže
od primárního paprsku. Odchylku odlišnou od násobku dvou stupňů určíme
interpolací. Svislé hyperboly slouží k odečtu úhlové vzdálenosti
vybraných difrakčních stop na girlandě, která odpovídá úhlu mezi
reciprokými vektory. Úhloměr na spodní straně nám umožňuje
odečíst úhlovou odchylku průmětu osy pásma (kolmice k rovině
reciproké mříže) od zvoleného referenčního směru, např.
svislici vyznačenou naexponovanými dírkami v kazetě. Postup
je podrobně popsán např. v knize Baretta [3, 4].
Obr.
5
Laueho metoda na odraz – reálné experimentální uspořádání s „Eulerovským“
držákem masivního krystalu.
 |
|
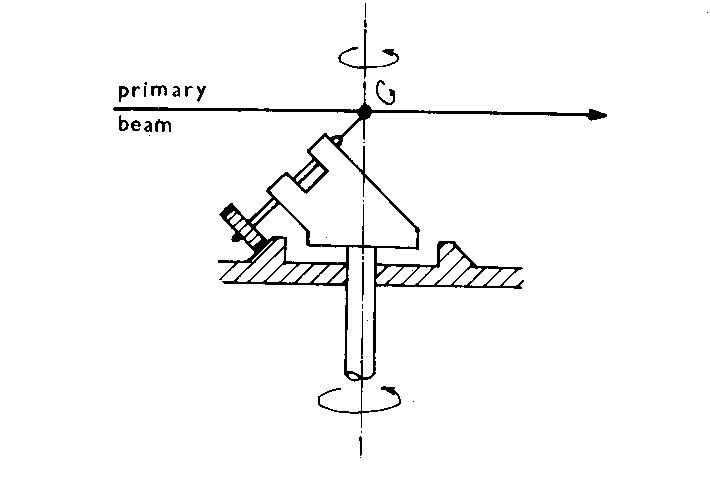
Obr. 6 |
Laueho metoda na odraz se používá pro orientaci monokrystalů za účelem zhotovení orientovaných vzorků vhodných tvarů (destiček, hranolků, prismat) potřebných pro různá fyzikální měření. Pro tento účel je nutno upevnit krystal do speciálního držáku, umožňujícího v potřebném rozsahu otáčení nejméně kolem dvou os a posuv vzorku ve dvou směrech. Musí být přenosný na pilu pro provedení orientovaných řezů. Držáky bývají obvykle konstruovány a vyráběny individuálně podle potřeb pracovišť a není vyjímkou používání několika typů držáků na stejném pracovišti. Vesměs se používají držáky s geometrií podobnou goniometrické hlavičce, s možností otáčení a naklápění, nebo se dvěma Eulerovskými kruhy - úplným c a neúplným w (obr. 6).
Postup orientace je následující: Upevníme krystal na držák, zpravidla natmelením, a zhotovíme zkušební snímek. V příznivém případě nalezneme difrakční stopu odpovídající některému význačnému směru. Jinak musíme krystal zkusmo přelepit, v případě nutnosti i opakovaně. V praxi lze často pro předběžnou orientaci využít i další vlastnosti krystalu - morfologii, štěpnost, optickou anizotropii. Pomocí Greningerovy sítě určíme odchylku vytipované difrakční stopy od středu snímku – otvoru pro kolimátor a spočítáme, o kolik je třeba otočit kruhy nebo kolébky držáku. Provedeme potřebné opravy a zhotovíme nový snímek. Pokud nebylo dosaženo správné orientace, znovu změříme odchylku a postup opakujeme. Lauegram krystalu orientovaného podle význačného krystalografického směru má odpovídající symetrii. Ukázky skutečných snímků na odraz jsou na obr. 7 a 8.
|
|
|
|
Obr. 7 |
Obr. 8 |
Pro zhotovení Laueho snímků používáme standartní nebo na míru zhotovené ploché kazety přizpůsobené příslušným nosičům – u nás univerzálním držákům Chirana. V zahraničí se používají kazety Polaroid, které lze kolimátorem prostě a jednoduše propíchnout.
Lauegram na průchod lze improvizovaně zhotovit na precesní komůrce
při nastaveném nulovém precesním úhlu a vypnutém pohybu.
Jakou
informaci můžeme pomocí Laueho metody získat? V prvé řadě je
nutno zdůraznit, že není principielně možné obdržet žádný
kvantitativní údaj, protože nelze určit, které vlnové délky se účastnily
difrakce pro danou stopu. Pokud máme krystal správně orientován, to jest
některý význačný krystalografický směr (reciproký vektor) je
paralelní s primárním paprskem, má difrakční obraz odpovídající
symetrii, například dvojčetnou, trojčetnou, čtyřčetnou.
Této symetrii je podřízeno rozložení girland i distribuce intenzit
difrakčních stop.
Pro správné určení symetrie je třeba, aby byl krystal co nejpřesněji orientován. V praxi totiž můžeme poměrně často narazit na pseudosymetrii. S ní musíme počítat u krystalů, jejichž struktura je odvozena deformací od některé výše symetrické ideální struktury. Příkladem je například LiNbO3 nebo LiTaO3, které mají rhomboedricky deformovanou perovskitovou strukturu [5] viz obr. 9, nebo korund (Al2O3), jehož rhomboedrická struktura je odvozena od kubické s nejtěsnějším směstnáním. Rhomboedrickou deformací kubické buňky zmizí tři ze čtyř trojčetných os. Lauegram krystalu orientovaného podle zmizelé trojčetné osy však vykazuje velmi výraznou pseudosymetrii a proto jej na první pohled lze zaměnit s lauegramem podle skutečné trojčetné osy. Teprve bedlivým zkoumáním přesně orientovaného snímku lze rozpoznat, že difrakční obraz má ve skutečnosti pouze bilaterální symetrii – vzhledem k tomu, že zůstává zachována jedna z rovin symetrie z původních tří, které se protínaly v trojčetné ose. V takové struktuře lze rovněž nalézt tři zmizelé čtyřčetné osy, ale žádnou skutečně zachovalou. Ze šesti dvojčetných os zůstávají tři zachovány a tři další zmizí. Dalším příkladem jsou některé tetragonální struktury perovskitového typu, u kterých bývá obtížné rozpoznat zachovalou a zmizelou čtyřčetnou osu.
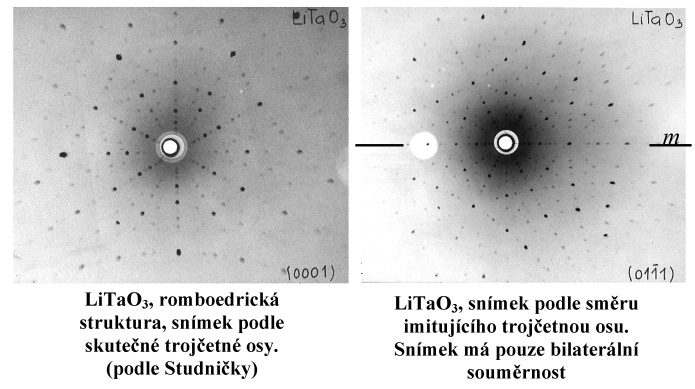
Obr. 9
Ukázka Lauegramů
na odraz – LiTaO3, rhomboedrický krystal, deformovaná perovskitová
struktura, demonstrace symetrie a pseudosymetrie. Podle Studničky [5].
Kromě popsaného použití se Laueho metoda někdy používá k posouzení kvality krystalu a jeho vhodnosti pro další měření. Špatná kvalita krystalu se projeví na tvaru difrakčních stop a vysoká mozaicita způsobí jejich rozštěpení. Ukázka takového snímku je na obr. 10.

Obr. 10
Ukázka
Lauegramu na odraz nedokonalého krystalu.
Společným znakem těchto metod je, že ke splnění Braggovy
podmínky dochází postupně, a za tímto účelem musí krystal vykonávat
vhodný pohyb. Metody vyžadují monochromatické záření. V praxi
postačí záření z běžné rentgenky filtrovavé b
filtrem.
Krystal je upevněn na goniometrické hlavičce v ose válcové
kazety a vykonává rotační kolem osy hlavičky. Na krystal dopadá ve
směru kolmém k ose hlavičky kolimátorem vymezený paprsek
monochromatizovaného (filtrovaného) záření. Pokud krystal pouze
osciluje ve vymezeném úhlovém oboru, jedná se o metodu oscilační,
pokud se otáčí kolem osy o plných 360°, jedná se o metodu rotační. Existují sice specielně
konstruované rotační komůrky, ale účelnější je použít
Weissenbergův goniometr (s odpojeným posuvem kazety), o kterém je pojednáno
v další kapitole.
Krystal musí být najustován tak, aby osa hlavičky (a rotace) byla totožná s vektorem přímé mříže. Na rotačním a oscialčním snímku jsou difrakční stopy soustředěny na rovnoběžných vrstevnicích, kolmých k ose hlavičky a kazety. Každá vrsevnice je zkolabovaným obrazem roviny reciproké mříže. Z Ewaldovy konstrukce (obr. 11) vyplývá, že n-tá vrstevnice je obrazem n-té roviny reciproké mříže, kolmé k vektoru přímé mříže, kolem kterého je krystal otáčen. Ukázka rotačního snímku je na obr. 12. Experimentální uspořádání pro rotační metodu (na Weissenbergově goniomeru) je na obr. 13.
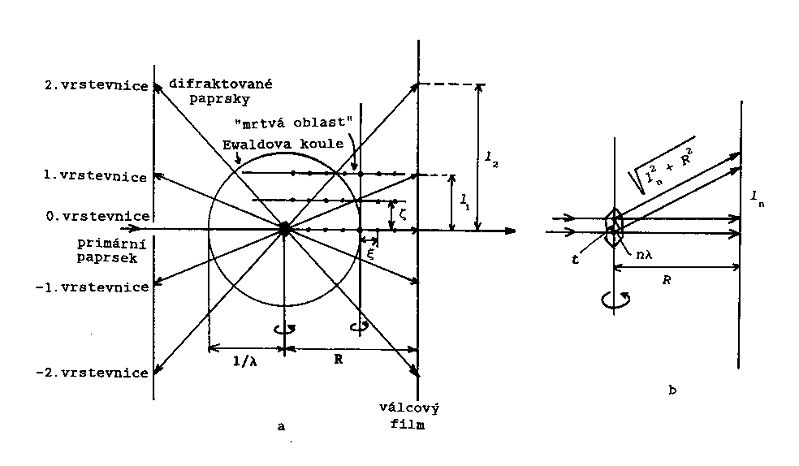
Obr. 11
Rotační
metoda – a) Ewaldova konstrukce, b) odvození vzorce (1) pro výpočet délky
přímého mřížkového vektoru.
 |
 |
|
Obr. 12 |
Obr. 13 |
Obraz reciproké mříže na rotačním snímku je zkreslený,
protože souřadnice difrakčních stop nejsou lineární funkcí souřadnic
bodů reciproké mříže, a zkolabovaný, protože jde o
projekci trojrozměrné mříže na dvojrozměrný film. Z Ewaldovy
konstrukce dále vyplývá, že u nenulových rovin reciproké mříže
existuje jistá „mrtvá“ oblast v blízkosti osy otáčení, nepřístupná
pro difrakci.
Důležitým údajem který lze z rotačního snímku vypočítat,
je délka přímého vektoru, podle kterého je krystal rotován.
Je-li krystal najustován podle některého vektoru základní buňky,
určíme tím příslušný mřížkový parametr. Délku přímého
vektoru určíme podle vzorečku:
|
t = (nl/ ln) √( ln2 + R2) |
(1) |
kde t je hledaná délka
vektoru (mřížková translace), ln je kolmá vzdálenost
n-té vrstevnice od nulté, R je poloměr kazety a l je vlnová délka použitého záření.
Pro popis reciproké mříže
pro tyto a následující metody je účelné zavést popis pomocí válcových
souřadnic x, j,
a z v reciprokém prostoru. x je délka průmětu radiusvektoru bodu reciproké mříře
do roviny kolmé k ose otáčení. j
je úhel, který tento průmět svírá se zvoleným referenčním
vektorem ležícím v nulté rovině reciproké mříže. z
je kolmá vzdálenost bodu reciproké mříže od nulté roviny. Hodnoty x
a z
lze vyjádřit buď v absolutních
jednotkách (Ĺ-1), nebo jako bezrozměrné veličiny. Při
studiu literatury je třeba dávat pozor, jakého způsobu autor používá.
Z předešlého vyplývá, že z
= n/t (v absolutních jednotkách). Souřadnici x
(pro nultou vrstevnici) určíme z modifikované Braggovy rovnice jako x
= (2 sin q)
/ l.
Pro hrubý odečet slouží Bernalova síť, uveřejněná např.
v [6, 7]. Nelze však určit souřadnici j,
protože chybí informace, při kterém úhlovém natočení krystalu došlo
k difrakci.
Metoda je podrobně popsána v monografii Buergera [6], dále v [10,
7, 8].
Pro justování krystalů pro metodu rotační a Weissenbergovu se
používá postup podle Umanského [11]. Krystal je nalepen na goniometrickou
hlavičku, zcentrován a nahrubo zjustován. Potom je pořízen oscilační
snímek (nefiltrovaným zářením) tak, aby jedna kolébka hlavičky
byla přibližně rovnoběžná s paprskem a druhá k němu kolmá.
Je vhodné vyznačit na snímku referenční čáru (např.
naexponováním stopy primáru při posuvu vozíčku s kazetou). Je-li
odchylka velká (zpravidla na počátku justační procedury) pořídíme
oscilační snímek pouze v dané poloze. Je-li odchylka malá, exponujeme
snímek dvakrát, ve dvou polohách otočených o 180° s různě
dlouhými expozicemi (2´
až 3´).Výsledkem
je zdeformovaný oscilační snímek, na kterém jsou vrstevnice zkřiveny,
popřípadě dvojexpozice takového snímku (obr. 14). Odečteme, ve
vzdálenostech x cca ±35
mm od středu snímku, odchylky Dl1
a Dl2
deformované nulté vrstevnice od "ideální polohy vrstevnice". Je-li
odchylka malá, určíme tyto hodnoty jako polovinu vzdálenosti slabě
a silně exponované vrstevnice. Při velké odchylce, kdy je vhodné
exponovat pouze v jedné poloze, odměříme hodnoty Dl1
a Dl2
od kolmice k referenční čáře, vedené středem snímku. Střed
snímku určíme buď jako bod, do kterého směřují difúzní
pásy od difrakčních stop, anebo si jej označíme naexponováním
stopy primáru při stojící kazetě. V krajním případě lze
"ideální polohu vrstevnice" určit zkusmo. 
Obr.
14
Ukázky
orientačních snímků demonstrujících postup justace od výchozího
stavu (snímek 1)
až po najustovaný krystal (snímek 3). Pro takovéto snímky se používají
jinak nevyužitelné odřezky filmů. Všimněte si referenční
čáry – stopy primáru, naexponované při posuvu kazety, která má
být kolmá k vrstevnicím na snímku najustovaného krystalu.
Příslušné
úhlové opravy e//
a e^
pro rovnoběžnou, respektive kolmou kolébku (míněn směr, kterým
se kolébka posouvá) činí (ve stupních):
|
|
(2) |
|
e^= (˝Dl1˝ ± ˝Dl2˝) (180/4p R sin 2q) |
(3) |
kde R je poloměr kazety a q
Braggův úhel, který určíme jako x/2R. Znaménka +
nebo –dosadíme do (2) a (3) podle toho, která složka rozjustování převažuje.
Smysl korekce určíme tak, aby posun kolébky "srovnal" zkřivenou
nultou vrstevnici. Po provedení příslušné korekce celý postup
opakujeme, v případě nutnosti i vícekrát, dokud se vrstevnice
exponované v obrácených polohách dokonale nepřekrývají.
Podrobně
je justační postup popsán například v [8]. Je účelné si pro
danou komůrku tabelovat funkce ( 180/4p
R sin2 q
) a (180/4p R sin
2q) pro poloměr používané komůrky. Příslušnými
hodnotami těchto funkcí vynásobíme ˝Dl1˝
+ ˝Dl2˝ a
˝Dl1˝
- ˝Dl2˝ a
dostaneme příslušné hodnoty korekcí.
Další
pomůckou používanou pro justáž krystalů je Kulpeho
"Kristalljustiergerat" neboli "Kulpeho kouzelná lampa" [12,
13]. Oscilační snímek se omotá kolem skleněného válečku,
uvnitř kterého je světelný zdroj a stínící clonka, která
vymezuje rozhraní světlo-stín, které je nutno stavěcími šrouby
ztotožnit s deformovanou nultou vrstevnicí. Jakmile se to podaří,
lze na stavěcích šroubech odečíst hodnoty korekcí.
3.2.1
Geometrie metody
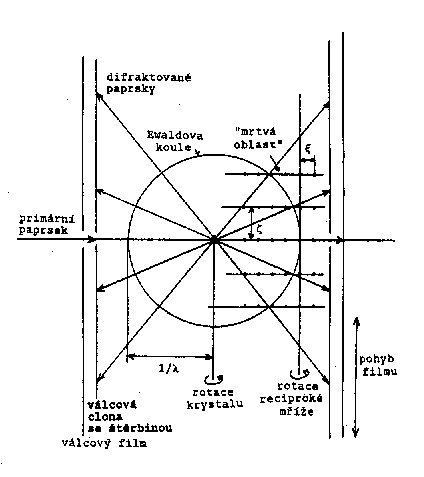 |
|
Obr. 15 |
Tato
metoda patří mezi metody s pohyblivým krystalem i filmem. Účelem
pohybu filmu je odlišení difrakčních stop, pro které nastala podmínka
pro difrakci v různém čase a při různé hodnotě
otočení krystalu. Krystal je upevněn na goniometrické hlavičce
v ose válcové kazety, která pojíždí na vozíku ve směru osy hlavičky
tak, že rotace krystalu je mechanicky spřažena s pohybem vozíku.
Pomocí válcové clony se štěrbinou je vymezena jedna vrstevnice Ewaldova
konsrukce je na obr. 15, detailní pohled na aparaturu se sejmutou kazetou na
obr. 16, uspořádání pro snímkování na obr. 17. Difrakční stopy
náležející vybrané vrstevnici jsou rozprostřeny po celé ploše filmu.
Obraz reciproké mříže je nezkolabovaný, ale zkreslený.
Jelikož reciproká mříž je útvar trojrozměrný a Weissenbergův
snímek dvojrozměrný, můžeme na jednom snímku zobrazit pouze jeden
řez reciprokou mříží. Proto je třeba zpravidla nutno pořídit
snímků více.
Zkreslení
je způsobeno růzností pohybu krystalu (rotace) a filmu (posun). Snímek
nulté vrstevnice pořizujeme v kolmém uspořádání jako při
rotační metodě, to jest s primárním paprskem dopadajícím kolmo k
ose rotace krystalu. U vyšsích vrtevnic ale vzniká "mrtvá" oblast
kolem průmětu počátku do roviny reciproké mříže (srv.
obr. 11 a 15).
|
|
|
Obr. 16 |
|
|
|
Obr. 17 |
Mrtvou oblast lze snadno odstranit použitím ekviinklinačního uspořádání (obr.18). Celým přístrojem pootočíme tak, aby primární paprsek svíral s rovinou reciproké mříže stejný úhel m jako difraktované paprsky.
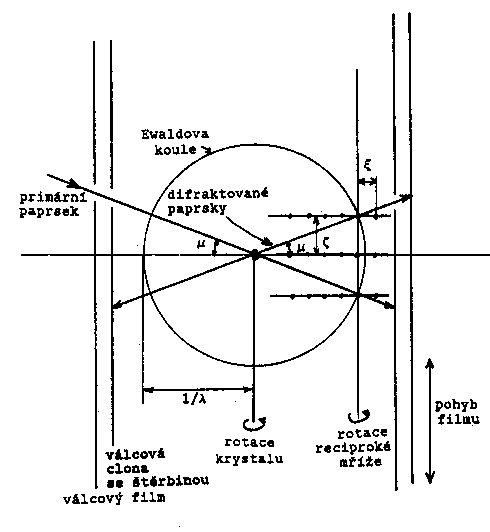 |
 |
|
Obr. 18 |
Obr. 19 |
Experimentální
uspořádání je patrné na obr. 19. Pro n-tou vrstevnici spočítáme
úhel m
ze vztahu:
|
sin m = nl / 2t |
(4) |
kde t je délka přímého vektoru ze vztahu
(1). Stěrbinu stínícího válce
posuneme z nulové polohy o vzdálenost s, danou vztahem:
|
sin m = nl / 2t |
(5) |
kde Rs je poloměr stínícího válce.
Weissenbergovy goniometry jsou uspořádány tak, že toto pootočení
umožňují. Ekviinklinačním uspořádáním nejen eliminujeme
mrtvou oblast, ale odstraníme další nepříjemné zkreslení
Weissenbergova snímku – esovitou deformaci centrálních přímek.
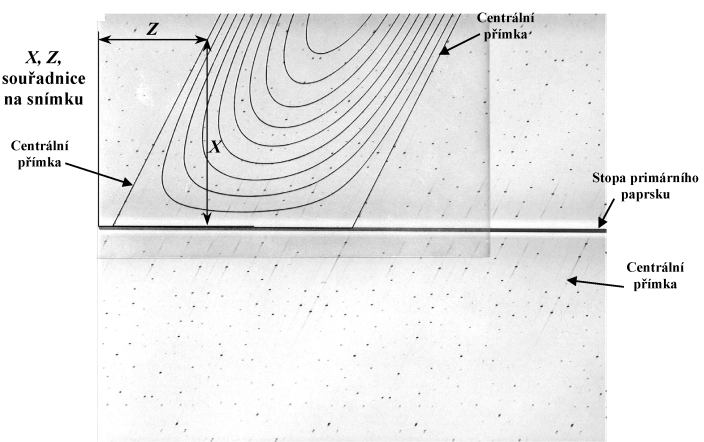
Na
Weissenbergově snímku (ukázku viz na obr. 20) se přímky reciproké
mříže jeví jako křivky ve tvaru nakloněného U, které
můžeme proložit difrakčními stopami. Přímky procházející
počátkem, resp. (u ekviinklinačních snímků vyšších
vrstevnic) průmětem počátku do vrstevnice se jeví na
Weissenbergově snímku jako šikmé přímky, které nazýváme přímkami
centrálními. Ty jsou vždy přítomné na snímku nulté vrstevnice, ale
mohou chybět na vrstevnicích vyšších, samozřejmě s vyjímkou
triviálního případu centrální přímky obsazené jediným bodem.
Stává se to v případě, když je síť bodů vyšší
vrstevnice posunuta vůči nulté, například u soustavy triklinické
nebo u monoklinické (zde s vyjímkou krystalu rotovaného dle dvojčetné
osy). Na Weissenbergově snímku konvenčně zavádíme dvě souřadnice
X a Z. Souřadnice Z je rovnoběžná se směrem
posuvu a její počátek volíme na levém okraji snímku (křivky tvaru
U se kloní doprava). Souřadnice X je k ní kolmá a její počátek
leží na myšlené pravolevé ose (v praxi jej musíme určit jako průměr
z X-ových souřadnic několika dvojic symetricky ekvivalentních
stop na protilehlých polovinách snímku). Nejpohodlněji určíme tyto
souřadnice pomocí komparátoru (mikroskopu) s posuvným stolečkem se
dvěma posuny na sebe kolmými. Pro usnadnění proměřování
je vhodné naexponovat stopu primárního paprsku během jednoho průběhu
kazety z jedné úvrati do druhé. Nelze ji sice brát jako počátek
souřadnice X, ale poslouží k správnému usazení snímku do
komparátoru. Zaveďme si dvě konstanty Cl a C2,
které přepočítávají souřadnice X na úhel q
a Z na souřadnici j. Pro poloměr
kazety 28.6 mm a spřažení posuvu s rotací 2°/mm platí Cl
= C2 = 2. Pro výpočet difrakčního úhlu a válcových
souřadnic bodů reciproké mříže platí následující vztahy:
|
2q = Cl X |
(6) |
|
x = (sinq cos m ) / (2l) |
(7) |
|
j = C2 Z - q |
(8) |
|
z = (2 sinm) / l |
(9) |
Je evidentní, že souřadnice z
je konstantní pro celou rovinu reciproké mříže. Všimněme si dále,
že volba souřadnice j je
odvislá od volby počátku souřadnice Z na snímku. Souřadnice
reprezentuje délku reciprokého vektoru. Ze souřadnic difrakčních
stop na centálních přímkách odpovídajících základním směrům
můžeme, je-li splněna podmínka rovnoběžnosti přímého a
reciprokého vektoru, spočítat příslušný mřížkový parametr
jako l/(nx), kde n je řád difrakce. Z rozdílu souřadnic
j
stop na centrálních přímkách, odpovídajícím význačným
směrům určíme reciproký úhel. Nejsou-li vyšší vrstevnice vůči
nulté posunuty, určíme i přímý úhel jako doplněk úhlu
reciprokého do 180°.
Weissenbergova
metoda si v kombinaci s rotační zachovává význam pro určení
mřížkových parametrů a prostorové grupy z charakteristického
vyhasínání. Metody jsou podrobně popsány v [6, 8], dále
též v [9, 10].
3.2.3 Rektifikace Weissenbergových
snímků
Interpretace Weissenbergových snímků vyžaduje vzhledem ke zkreslení určitou zkušenost a může být pro začátečníka obtížná. Proto se vyskytly snahy odstranit zkreslení a vytvořit plnohodnotný, nezkreslený obraz reciproké mříže, to jest snímek rektifikovat. Poměrně primitivním způsobem se o toto pokusil Hybler et al. [14]. V poslední době vytvořil Weber [15] program dwb99 pro rektifikaci Weissenbergova snímku sejmutého scanerem a uloženém do počítače ve vhodném grafickém formátu (např. tiff). Výsledek je na obrázku 21. Program bohužel nebyl dosud doveden do podoby vhodné pro všeobecné použití.
Obr. 21
3.3.1 Popis metody
Tato metoda byla vyvinuta ve snaze získat nezkolabovaný a nezkreslený obraz roviny reciproké mříže. Proto je nezbytné, aby krystal i film vykonávaly shodný pohyb. Jedním ze způsobů, jak toho bez mechanické kolize dosáhnout, je pohyb precesní, při kterém libovolný mřížkový vektor opisuje plášť kužele.
 |
|
Obr. 22 |
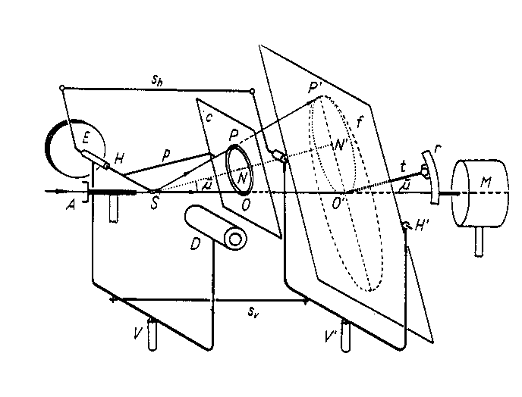
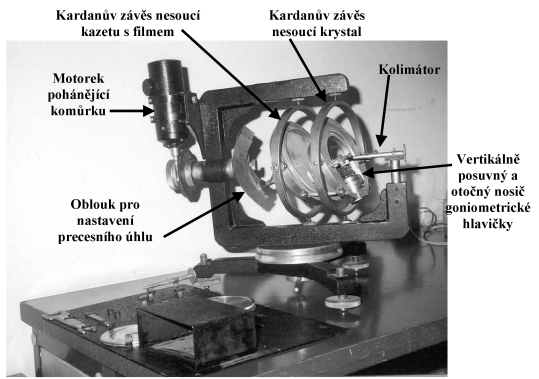
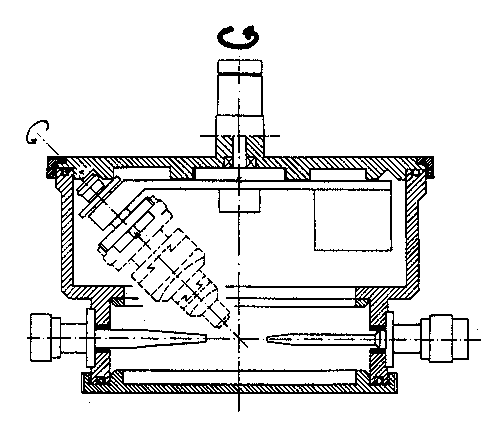
Krystal je upevněn na goniometrické hlavici ve středu Kardanova závěsu. Tento je spojovacími elementy spřažen s dalším Kardanovým závěsem, který nese plochou kazetu s filmem. (viz obr. 22). Vzdálenost M mezi středy Kardanových závěsů nazýváme přístrojovou konstantou precesní komůrky. Nosič kazety je z opačné strany spojen s čepem, který zapadá do ložiska které je pevnou částí elementu. Ten je možné posouvat v drážce půloblouku pevně spojeného s hnacím hřídelem a tím nastavit a aretačním šroubem zafixovat precesní úhel m. Se závěsem filmu je pevně spojen držák nesoucí kovovou clonku s mezikružím pro vymezení difraktovaných paprsků náležejících jedné rovině reciproké mříže. Motorek otáčí půlobloukem, který nutí krystal i film vykonávat precesní pohyb. Goniometrická hlavička je nasazena na otočném držáku se stupnicí. Držák umožňuje jednak justaci (viz dále ) a jednak nastavení libovolné (nulté) roviny reciproké mříže rovnoběžné s osou hlavičky do polohy pro snímkování. Na schématu je klasické uspořádání dle Buergera [16] s vodorovnou osou hlavičky. Skutečnou komůrku zobrazuje obr. 23. Možné je i alternativní uspořádání se svislou osou hlavičky dle Hanice [17] (obr. 24). Další modifikací je zpětně reflexní precesní komůrka dle Riedra [9, 18].
|
|
|
Obr. 23 |
 |
|
Obr. 24 |
Pro
registraci nulté roviny reciproké mříže je kazeta s filmem umístěna
tak, aby střed Kardanova závěsu - mrtvý bod byl ve středu
filmu. Pro registraci vyšší roviny je třeba kazetu posunout směrem
ke krystalu o Mz.
Souřadnice z má stejný
význam jako v předešlé kapitole a u precesní metody se konvenčně
volí kolmo ke snímkované rovině a v bezrozměrných jednotkách.
Hodnotu z
určíme ze snímku cone-axis (viz dále) nebo z precesního snímku nulté
vrstevnice krystalu otočeného o 90°. Na snímku
vyšší vrstevnice vzniká kolem středu filmu oblast nepřístupná
difrakci. Na obr. 25 je graficky znázorněna
dostupnost reciprokého prostoru v závislosti na m,
x,
a z
(x
také v bezrozměrných jednotkách). Z tohoto mj. vyplývá zásadní
nedostatek precesní metody - špatná dostupnost reciprokého prostoru. Tento
nedostatek lze do jisté míry kompenzovat použitím kratší vlnové délky
(např. MoKa).
3.3.2 Interpretace precesních snímků
Interpretace
precesních snímků je velmi jednoduchá, protože snímek je přesným
obrazem reciproké mříže v měřítku daném vlnovou délkou a přístrojovou
konstantou M - vzdáleností vzorek-film. U běžných komůrek
je M = 60 mm. Souřadnici x
bodu reciproké mříže určíme jako
|
x = x / (Ml) |
(10) |
kde x je vzdálenost střed snímku-difrakční
stopa. Souřadnici j prostě
odměříme úhloměrem na snímku. Vztah (10) používá absolutní
jednotky (Ĺ-1), pro bezrozměrné x platí x
= x / M . V praxi se pro proměřování precesních
snímků používá zvláštní otočný stoleček s kulatým okénkem,
úhlovou stupnicí a skleněnou destičkou s ryskou, připevněnou
na posuvném měřítku (obr. 26). Snímek nalepíme na skleněné
okénko a prosvětlíme zespoda. Pomocí rysky odměřujeme kolmé
vzdálenosti řad difrakčních stop. Na úhlové stupnici odečteme
úhlové polohy řad difrakčních stop a z jejich rozdí1u určíme
úhel, který svírají. Je-li splněna podmínka, že vyšší vrstevnice
není posunuta vůči nulté, (u orthorhombické a vyšší symetrie, též
u monoklinické kolmo k dvojčetné ose), lze určit příslušný
přímý mřížkový parametr jako Ml/d*,
kde d* je příslušná rozteč. Není-li tato podmínka splněna,
je interpretace mnohem složitější a přesahuje rámec této práce.
Velmi vhodná je precesní metoda k určování prostorové grupy, pro
studium dvojčatění a orientovaných srůstů a také k odhalení
některých vlastností krystalů.
|
|
|
Obr. 26 |
Ukázka
běžného precesního snímku je na obr. 27. Možnosti precesní metody dobře
ilustruje snímek roviny hhl dvojčete, které obsahuje
rhomboedrickou buňku v obversním i reversním postavení (obr. 28).
|
|
|
|
Obr. 27 |
Obr. 28 |
|
|
|
|
Obr. 29 |
Obr. 30 |
 |
|
Obr. 31 |
Zde je popsán zjednodušený, avšak
v praxi vyhovující justační postup. Je potřebné aby byl
krystal přibližně orientován tak, aby rovina reciproké mříže,
kterou chceme studovat byla přibližně rovnoběžná s jednou kolébkou
goniometrické hlavičky. Nastavíme malý precesní úhel (m
≈ 10-12°)
a naexponujeme zkušební snímek bez mezikruží a s nefiltrovaným zářením.
Po vyvolání nalezneme na snímku přibližné kruhovou oblast, tvořenou
pásy vzniklé difrakcí polychromatického záření směřujícími
paprskovitě ze středu snímku do kraje oblasti, na které jsou ostře
zakončeny (viz obr. 31). V pásech jsou patrné difrakční stopy
čar Ka
i Kb
. Krystal je správně najustován, když je tato oblast přesně
kruhová a všechny paprsky končí ve stejné vzdálenosti od středu.
Čím více je krystal rozjustován, tím více je tato oblast excentrická
a deformovaná do tvaru srdíčka.
Pro stanovení opravy je nutno nalézt
tři korekce: e//
kolébky rovnoběžné s paprskem, eD
pro korekci otočení držáku goniometrické hlavičky a konečně
e^
kolébky kolmé k paprsku. Prvními dvěmi korekcemi uvedeme krystal do
takové polohy, aby rovina reciproké mříže byla rovnoběžná s
filmem a tudíž byla kruhová oblast na justačním snímku přesně
zcentrována. Třetí korekce slouží k tomu, abychom význačný
vektor přímé mříže dostali do osy hlavičky a umožnili snímkování
dalších rovin reciproké mříže po patřičném otočení
hlavičky kolem tohoto vektoru, bez nutnosti dalšího dojustování.
Další postup je ne zcela korektním
zjednodušením postupu dle Buergera, který však v běžné praxi
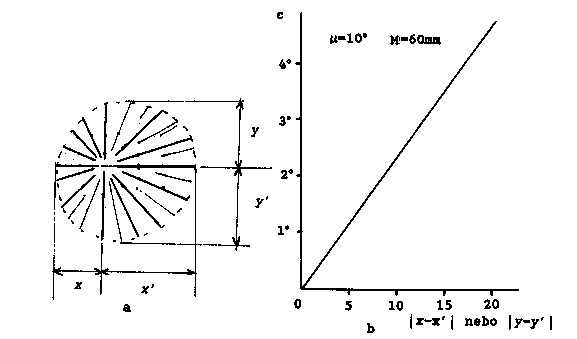
postačí. Změřme vzdálenosti
x, x' a y, y' podle obr. 31a, a spočtěme hodnoty
˝x
-x'˝
a ˝y
-y' ˝.
Úhlové korekce odečteme z grafu na obr. 31b pro daný úhel m.
Pro uspořádání dle Buergera určímé e//
z ˝x -x'˝, eD
z ˝y -y' ˝, u uspořádání dle Hanice je
tomu naopak. Krystalem musíme pootočit opačným směrem, než
kterým je posunuta kruhová oblast. Poslední korekci e^
určíme jednoduše úhloměrem, pokud je na filmu vyznačen směr
osy hlavičky, například naexponovanými stopami po dírkách v kazetě.
Korektní justační postup je podrobně popsán Buergerem [16] a
Riederem [9], který uvádí i variantu pro hlavičku s kolébkami v diagonálním
uspořádání. Program pro počítače PC, umožňující spočítat
korekce a najustovat krystal při jakémkoli nastavení hlavičky
sestavil Rieder [19].
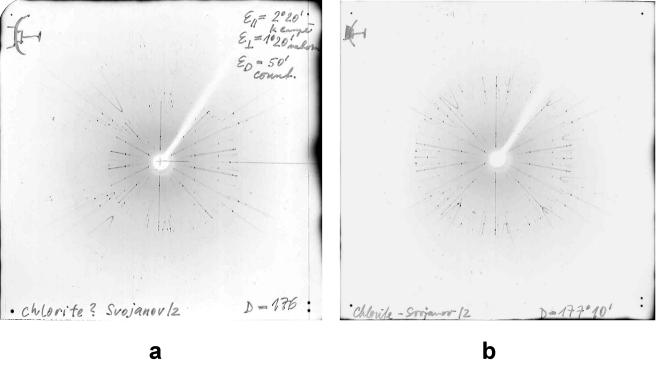
Obr. 32
Všimněme
si ještě některých vlastností justačních snímků. Kromě
kruhové oblasti odpovídající nulté rovině se na snímku mohou
vyskytovat (není-li z
příliš velké) difrakční stopy z vyšších rovin. Zpravidla se
vyskytují na difúzních pásech ve tvaru protáhlých smyček. Jejich
rozložení na snímku již zorientovaného krystalu dává informaci o symetrii
nenulových rovin reciproké mříže, neovlivněnou, podobně jako
u lauegramů a snímků cone-axis (viz dále), Friedelovým zákonem. Na
obr. 33a je justační snímek trigonálního krystalu s trojčetnou
osou kolmou k rovině filmu, na obr. 33b s trojčetnou osou
rovnoběžnou s rovinou filmu.
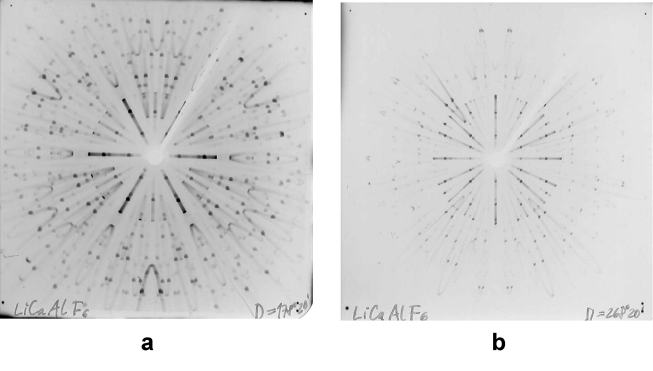
Obr. 33
Ukázka
orientačních snímků již najustovaných krystalů. LiCaAlF6,
trigonální krystal. a) trojčetná osa kolmá k rovině snímku - uspořádání
difusních smyček prozrazuje trojčetnou symetrii b) trojčetná
osa rovnoběžná s rovinou snímku (svislá).
I
při justování se lze setkat s potížemi. Pokud je reciproká mřížka
příliš hustá, může se na zkušebním snímku vyskytnout několik
překrývající se kruhových oblastí a je obtížné rozhodnout, na
kterou je nutno krystal najustovat (obr. 34a). Ukázka snímku nekvalitního
krystalu, nevhodného pro další studium je na obr. 34b.
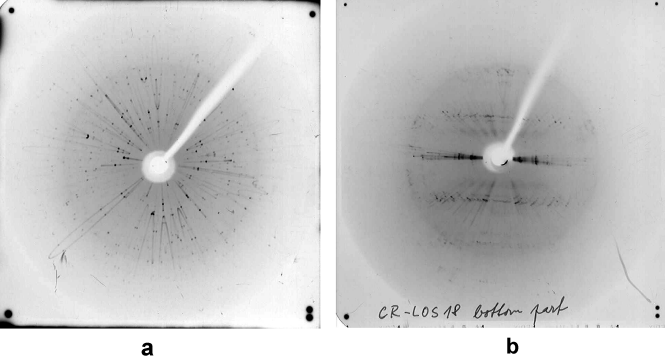
Obr.
34
Problematické
orientační snímky. a) na snímku je patrné více kruhových oblastí, a
nelze rozpoznat, která je „ta pravá”. b) snímek nekvalitního krystalu,
nevhodného pro další studium.
 |
|
Obr. 35 |
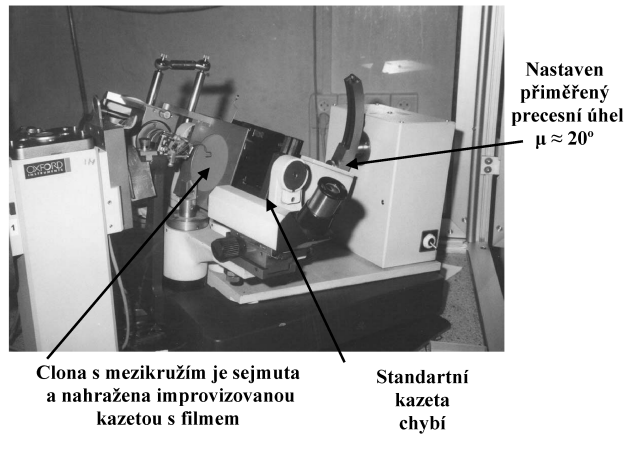
Jako
pomocná metoda pro precesní je používána metoda cone-axis. Uspořádání
je shodné, ale film je ve speciální kazetě umístěné místo clonky
s mezikružím v držáku pevně spojeným se závěsem krystalu (obr.
35). Během precesního pohybu difrakční kužely nekloužou po filmu,
ale zůstávají zafixovány. Na snímku tvoří difrakční stopy
soustředné kroužky, odpovídající jednotlivým difrakčním kuželům,
které zase odpovídají rovinám reciproké mříže. Tyto kroužky jsou
obdobou vrstevnic na rotačním snímku a proto je vypovídací schopnost
metody obdobná. Obraz reciproké mříže je v tomto případě
jak zkreslený, tak zkolabovaný. Kroužek nulté vrstevnice je
zpravidla intenzivnější než ostatní. Vzhledem k dosažitelnosti
reciprokého prostoru (srv. obr. 25) převažují kroužky vně nultého,
kroužky uvnitř nultého se vyskytují vzácně, při dostatečně
malém z. Z rozložení
stop na nenultém kroužku lze usoudit na symetrii příslušné roviny
reciproké mříže. Friedelův zákon se neuplatní, protože difrakční
stopa na n-tém kroužku má svého Friedelovského dvojníka na -n-tém
kroužku (zpravidla nezobrazeném). Ukázka snímku je na obr. 36. Snímek
cone-axis poskytne tedy obdobnou informaci jako lauegram. Lze z něj spočítat
souřadnici z
(v Ĺ-1) pro n-tou rovinu reciproké mříže podle
vztahu:
|
z = {cos m - cos[arctg(rn/s)] }/λ |
(11) |
kde rn je poloměr n-tého
kroužku a s vzdálenost vzorek-film (prakticky se používá s
= 30 mm při m
= 20°).
Připomeňme, že t = 1/z
je délka přímého vektoru kolmého k soustavě rovin reciproké mříže,
na které máme najustováno. Oproti rotační metodě je výpočet
méně přesný – chyba je větší zhruba o jeden řád.
Metoda má proto spíše význam pro kontrolu – odhalení případné
„zapomenuté“ roviny reciproké mříže, jejíž existence vede ke
zdvojnásobení některého původně nalezeného (přímého) mřížkového
vektoru.
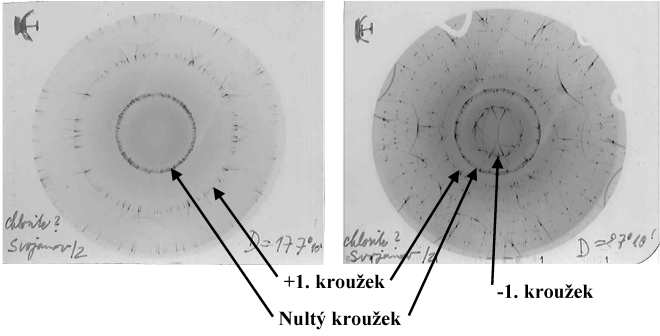
Obr. 36
Ukázky snímků
cone-axis.
3.3.5 Simulace
precesních snimků z difraktometrických dat
Pokrok
v difraktometrii a v rozvoji softwaru umožnil vytvořit
nezkreslený obraz reciproké mříže
pomocí počítačové rekonstrukce a tímto způsobem precesní
metodu do jisté míry nahradit. Jednou z možností je schematická
simulace precesního snímku ze souboru měřených difrakcí, kde
jsou difrakční stopy znázorněny plnými kroužky jejichž velikost
odpovídá intenzitě difrakce. Takto jsou vybaveny balíky programů
pro zpracování difraktometrických dat nebo strukturní analýzu, např.
soubor programů JANA2000 [20]. Ukázka je na obr. 37. Dokonalejším způsobem
je počítačová rekonstrukce vybraného řezu reciprokou mříží
z dat získaných pomocí plošně citlivého detektoru. Toto umožňuje
program CrysAlis zpracovávající data z difraktometru Xcalibur od firmy
Oxford Diffraction [21]. Tímto způsobem lze získat plnohodnotnou obdobu
precesního snímku (obr. 38).
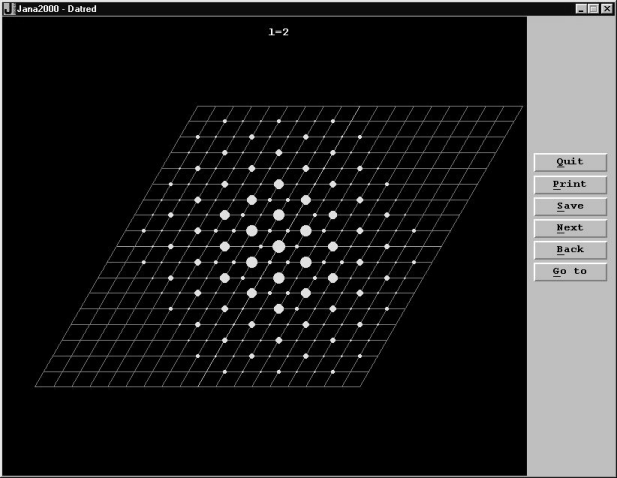 |
|
|
Obr. 37 |
Obr. 38 |
3.4 Ostatní metody: DeJong
-Boumanova, Sauterova a Schieboldova
Metoda
DeJong-Boumanova představuje druhou možnost registrace nezkolabovaného
a nezkresleného obrazu
rovin reciproké mříže. Schéma metody je na obr. 39. U spořádání
je obdobné jako při ekviinklinační Weissenbergově metodě
(srv. obr. 18), ale difraktované paprsky vymezené mezikružím jsou zachycovány
na plošný film kolmý k ose rotace a otáčející se synchronně s
krystalem. Při registraci nulté vrstevnice by však došlo k mechanické
kolizi - film by musel ležet ve stejné rovině jako krystal - a proto se v
tomto případě používá uspořádání antiekviinklinační.
Tato metoda, navzdory své relativní jednoduchosti, je daleko méně rozšířena
nežli precesní. Jistou oblibu získala v bývalém SSSR, kde posloužila v poválečném
rozvoji krystalografie a kde byla příslušná komůrka komerčně
produkována pod názvem: „Камера
для
фотографирования
обратной
решетки“. Existuje též kombinovaná
precesní a DeJong-Boumanova komůrka, tzv. Reciprocal Lattice Explorer,
který vyráběla firma Stoe (obr. 40).
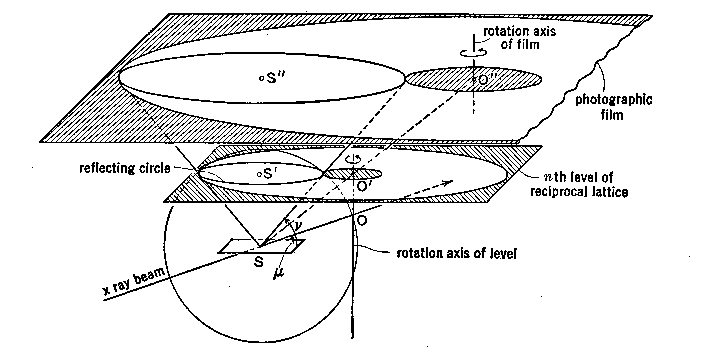
Obr. 39
Metoda
DeJong-Boumanova – schema. Podle Buergera [6].

Obr. 40
„Reciprocal
Lattice Explorer” firmy
Stoe. a) uspořádání pro metodu DeJong-Boumanovu b) uspořádání
pro metodu precesní.
Metody
Sautera a Schiebolda byly vyvinuty ve 30. letech a z dnešního hlediska se
jeví jako slepá ulička vývoje. Schéma obou metod je na obr. 41. Obě
poskytují nezkolabovaný, avšak zkreslený obraz roviny reciproké
mříže. Princip Sauterovy metody je následující: krystal se otáčí
jako u rotační metody a difraktované paprsky vybrané roviny reciproké mříže
vymezené štěrbinou jsou registrovány na plochý film, otáčejíci
se podle osy kolmé k ose otáčení hlavičky. Metoda trpí
zkreslením obrazu reciproké mříže a špatnou dostupností reciprokého
prostoru – horší než metoda Weissenbergova. Ukázka snímku je na obr. 42.
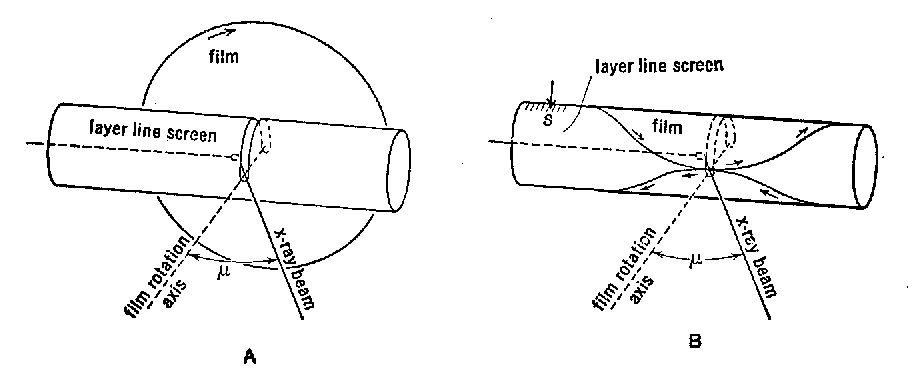 |
|
Obr. 41 |
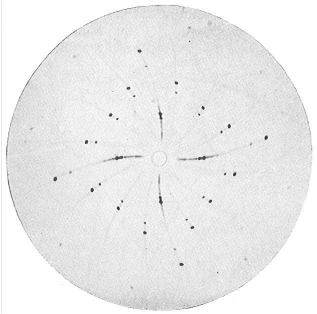 |
|
Obr. 42 |
U
Schieboldovy metody se kruhový film otáčel v zakřivené (válcové)
ploše koaxiální s osou rotace krystalu. To sice zlepšilo dostupnost
reciprokého prostoru, ale na druhé straně činilo problémy s poškozováním
filmu v důsledku otírání. Podrobnosti o těchto metodách
nalezne čtenář v [6] a [9].
K malému
úspěchu Sauterovy metody prý přispěla také skutečnost, že
zkreslení obrazu reciproké mříže poněkud připomíná hákový
kříž (srv. obr. 42).
V dobách před nástupem difraktometrů byly filmové komory - Weissenbergova, v menší míře precesní, používány ke sběru dat pro účely strukturní analýzy. Intenzity difrakcí byly odhadovány vizuálně pomocí srovnávací škály. Určitým pokrokem bylo fotomerické proměřování difrakčních stop na snímcích. Zde se ale objevila jedna potíž – pro tento účel bylo nutné integrovat intenzitu přes celou plochu difrakční stopy. Řešením tohoto problému je „rozmazání“ difrakční stopy ve dvou rozměrech pomocí speciálního mechanismu během expozice. Popis integrujícího Weissenbergova goniometru je v [22], precesní komůrky v [16]. Princip metody je patrný z obrázku 43. Je zřejmé, že uprostřed rozmazané stopy je intenzita úměrná součtu dílčích intenzit podél profilu stopy a lze ji jednoduše změřit fotometrem v jednom bodě. Za tím účelem byly vyráběny filmové komůrky s odpojitelným integrujícím mechanismem. Jsou tak vybaveny i komůrky na obr. 16 a 23, ale autor jej nikdy nepoužil. S rozvojem difraktografů ztratil tento způsob sběru dat význam a patří nenávratně do historie.
 |
 |
|
Obr. 43 |
Obr. 44 |
3.6
Gandolfiho metoda
Všechny
dosud popsané metody si kladly za cíl registrovat difrakce jednotlivých mřížkových
rovin a pokud možno je separovat. Gandolfiho metoda řeší jiný problém
– jak pořídit práškový snímek, pokud je k dispozici pouze
monokrystal. S takovou situací se často setkávají mineralogové zápasící
s nedostatkem studijního materiálu.
 |
|
Obr. 45 |
Podstata
klasické Debye–Scherrerovy metody spočívá v tom, že se v polykrystalickém
vzorku předpokládá dostatečné množství zrn v dostatečném počtu
orientací na to, aby koncové body každého reciprokého vektoru současně
vytvořily souvislou kulovou plochu. Tyto plochy potom protínají Ewaldovu
kulovou plochu v soustavě kružnic, takže difraktované paprsky vytvoří
soustavu koaxiálních kuželů, které protnou cylindrický film v
charakteristických debyeovských "kroužcích ". Gandolfiho metoda
dosahuje stejného efektu při použití jediného monokrystalu, který se
pomocí důmyslného mechanismu dostává do
potřebných orientací postupně. Namísto běžného nosiče
kapiláry s práškovým vzorkem, jak jej známe z běžné
Debye–Scherrerovy komůrky je umístěn otáčivý nosič, na
kterém je umístěna tyčinka se vzorkem tak, že její osa svírá s osou
komůrky úhel 45° (obr. 44). Některé komůrky novější
konstrukce jsou vybaveny nosičem standartní goniometrické hlavice (obr.
45). Tyčinka se vzorkem se otáčí kolem své osy, nebo osy
goniometrické hlavice a současně vykonává precesní pohyb
kolem osy komůrky.
I při
tomto složitém uspořádání zůstává část reciproké mříže
nepřístupná pro difrakci a proto je vhodné exponovat snímek
nadvakrát. Toho lze dosáhnout buď přelepením krystalu, nebo pořízením
první a druhé expozice při dvou extrémních polohách spodní kolébky
goniometrické hlavičky. Podrobně je metoda popsána a diskutována
v [23], a dále v [24]. Vzorek samozřejmě nemusí být nutně monokrystal, metodu lze s výhodou použít, pokud
je k dispozici např. shluk malých krystalů, nebo malé množství
prášku a dokonce v takovém případě funguje lépe.
Helliwel, J.R., Single Crystal X-ray Techniques. In: International Tables for Crystallography. Dordrecht/Boston/London 1992, pp. 26-41. Kluwer Academic Publishers.
Amorós, J.L., Buerger, M.J., Amorós, M.C. de: The Laue Method. New York-San Francisco-London 1975, Academic Press.
Barett, Ch. S.: Structure of Metals. New York- Toronto -London 1952, McGraw Hill Book Company.
Barett, Ch. S.: Struktura kovů. Praha 1959, Nakl. ČSAV (Překlad předešlé knihy).
Studnička, V.: Hodnocení základních materiálů elektroniky použitím rtg metod. Výzkumná zpráva č. 1620 13 712/3, TESLA VÚST A.S.Popova, Praha 1982.
Buerger, M.J.: X-Ray Crystallography. London 1942, Wiley & Sons.
Chojnacki, J.: Základy chemické a fyzikální krystalografie. Praha 1979, Academia.
Valvoda, V., Polcarová, M., Lukáč, P .: Základy strukturní analýzy. Praha 1992, Univerzita Karlova.
Rieder, M.:Přístroje s pohyblivým filmem. Sborník kolokvia "Experimentální techniky v rentgenové a neutronové analýze" Bechyně 1981.
Slavík, F., Novák, J., Kokta, J.: Mineralogie. Praha 1974, Academia (5. přepracované vydání).
Umanskij, M, M.: Zavodskaja laboratorija 13 (1950) 696.
Kulpe, S.: Acta Crystallogr. 16 (1963) 837-838.
Kulpe, S.: Acta Crystallogr. 21 (1968) 286-289.
Hybler, J., Syneček V., Marek V.: Czech. Journ. Phys. B27 (1977) 1129-1138.
Weber, T.: dwb99. Program to rectify Weissenberg-photographs to reciprocal space coordinates. Laboratorium für Kristallographie, Universität Bern, Schweiz, 1999.
Buerger, M.,J.: The Precession Method in X-ray Crystallography. New York-London-Sydney 1964, John Wiley & Sons.
Hanic, F.: Matematicko-fyzikálny časopis SAV 6 (1956) 21-29.
Rieder, M.: Z. Kristallogr. 151 (1980) 153-168.
Rieder, M.: PREORI, program pro justáž krystalů pro precesní metodu. (1993)
Petříček, V., and Dušek, M.: The crystallographic computing system JANA2000. Institute of Physics, Praha, Czech Republic, 2000.
CrysAlis RED. CCD data reduction program, Oxford Diffraction (Poland), 2002.
Wiebenga, E.H., Smits, D.W. : Acta Crystallogr. 3 (1950) 265-267.
Gandolfi, G.: Mineral. Petrogr. Acta 13 (1967) 67-74.
Ďurovič, S., Hybler, J.: Monokryštálové
filmové metody. Sborník kolokvia: Experimentální techniky v rentgenové
a neutronové strukturní analyze. Ostrava 1994