J. Hrdý
Fyzikální ústav AV ČR , Na Slovance 2, 182
21 Praha 8, Česká republika
Monochromatizací rentgenového záření rozumíme vymezení určitého intervalu vlnových délek Dl v okolí jisté vlnové délky l z dopadajícího spektra záření. Přístroj, kterým se tak děje se nazývá monochromátor. Ten může pracovat jen na jedné fixní vlnové délce l, ale častěji umožňuje vlnovou délku ladit v určitém rozmezí. Takový laditelný monochromátor pak má funkci i rentgenového spektrometru.
Princip monochromatizace závisí na vlnovém oboru. Pro tvrdé rentgenové záření se používají krystalové monochromátory, zatímco pro měkké rentgenové záření se používají mřížkové monochromátory (těmi se zde zabývat nebudeme). V poměrně široké oblasti zasahující jak do tvrdé, tak i do měkké části spektra jsou k monochromatizaci používány multivrstvy. Volbu typu monochromátoru ovlivňuje i požadovaná velikost intervalu Dl..
Praktická realizace monochromátoru závisí i na typu zdroje záření. Záření z rentgenové lampy se například v mnohém liší od rentgenového synchrotronového záření. Liší se v úhlové vyzařovací charakteristice, výkonu, polarizaci. Tomu všemu se musí konstrukce monochromátoru přizpůsobit.
Vymezení určitého intervalu Dl pro určitou vlnovou délku l není zpravidla jediným požadavkem kladeným na monochromátor. Často je třeba splnit ještě další požadavky, jako například: monochromátor musí vytvářet lineárně nebo i kruhově polarizované záření, monochromátor musí propouštět kruhově polarizované záření na něj dopadající, vystupující záření musí být fokusované, poloha vystupujícího svazku musí být nezávislá na vlnové délce, musí být zachována koherence monochromatizovaného záření a konstrukce monochromátoru musí respektovat značný výkon ve svazcích synchrotronového záření.
Rozlišovací schopnost R je definována jako poměr l/Dl = E/DE, kde E je energie fotonů. Mezi l a E platí vztah
|
E[eV] = 1240 / l [nm] |
(1) |
a
|
l/Dl = E/DE |
(2) |
Je zřejmé, že čím je větší rozlišovací schopnost, tím je nižší intenzita monochromatizovaného paprsku. Je proto třeba volit rozlišovací schopnost takovou, jakou potřebujeme, nikoliv větší. Pro některé účely stačí monochromatizovat tak, aby prošla celá spektrální čára (R je řádu 103) či dokonce a1,2 dublet, jindy je požadována rozlišovací schopnost řádově 107 nebo i větší.
Od rozlišovací schopnosti je třeba odlišit disperzi D. Předpokládejme, že nastavení vlnové délky závisí na nastavení určité veličiny x, kterou může být poloha štěrbiny, či úhel natočení krystalů apod. Disperze D je pak definována jako
|
D = dx / dl . |
(3) |
Obě veličiny, R a D, spolu přímo nesouvisí. Máme-li vysokou rozlišovací schopnost, pak můžeme rozlišit některé detaily např. v absorpčním spektru či na difrakční křivce. Vysoká disperze pak znamená menší nároky na mechanickou přesnost aparatury.
Nastavením monochromátoru na určité x nastavujeme záření vystupující z monochromátoru na určitou vlnovou délku. Toto záření pak dopadá na vzorek a po interakci s ním dopadá do detektoru. Někdy však může na vzorek dopadat celé široké spektrum záření a to po interakci se vzorkem také dopadá do detektoru. Použijeme-li ale detektor fotonů, u nějž je napěťová amplituda elektrického pulsu úměrná energii fotonů a současně amplitudový analyzátor pulsů, pak si nastavením určité amplitudy pulzů vlastně nastavujeme, či vybíráme určitou vlnovou délku a ostatní vlnové délky ignorujeme. Pak mluvíme o tzv. energetické disperzi. Je to metoda rychlá, ale rozlišovací schopnost je malá.
Při nastavení monochromátoru na určitou vlnovou délku L a jeho osvícení zářením o konstantní spektrální intenzitě (nezávislé na l), lze spektrální intenzitu monochromatizovaného záření popsat funkcí Z(l-L), obecně závislou na L, jejíž hodnoty se podstatně liší od nuly pouze v okolí l = L. Pološířka této funkce je výše uvedená hodnota Dl. Funkce Z je pak instrumentální zkreslovací funkce nebo též spektrální okno. Proměřujeme-li např. nějaké spektrum, pak naměřené spektrum je konvolucí skutečné spektrální intenzity a zkreslovací funkce. Je užitečné znát tvar funkce Z, abychom mohli provést dekonvoluci naměřené křivky a dopracovat se tak ke skutečné hledané spektrální intenzitě.
Z důvodu omezeného rozsahu je výklad spíše kvalitativní. Cílem je především pochopení principu a podání celkového přehledu o metodách monochromatizace, a to jak v klasických laboratořích, tak i u zdrojů synchrotronového záření.
V některých případech, zejména při použití velice intenzivního synchrotronového záření, dochází k nežádoucímu zahřívání rentgenooptických elementů. Je proto účelné odstranit ze spektra záření dopadajícího na monochromátor nepotřebnou část. Toho se dociluje použitím absorpčních filtrů a zrcadel.
Zeslabení intenzity rtg. záření po průchodu prostředím o tloušťce t je dáno exponenciálním vztahem
|
I(t) = I0exp(-mt), |
(4) |
kde m je tzv. lineární absorpční koeficient [1, 2] závislý na vlnové délce záření a materiálu prostředí a I0 je intenzita záření dopadající na absorbér. Závislost absorpčního koeficientu na vlnové délce je schematicky znázorněno na obr. 1. Se zvyšující se energií fotonů, tj. zmenšující se vlnovou délkou absorpční koeficient klesá. Obecně tedy filtry odstraňují dlouhovlnnou část spektra.Dosáhne-li energie fotonů hodnoty postačující k vyražení elektronu z některé atomové hladiny, dojde k náhlému vzrůstu absorpčního koeficientu a při dalším zvyšování energie fotonů m opět klesá. Uvedený náhlý vzrůst absorpčního koeficientu nazýváme absorpční hranou. Vlnové délky absorpčních hran klesají s rostoucím protonovým číslem.
Obr. 1
Příklad závislosti absorpčního koeficientu na vlnové délce.
Zvolením vhodného materiálu a tloušťky tak, že krátkovlnná hranice potřebného úseku spektra leží v oblasti absorpční hrany, pak kromě dlouhovlnné (měkké) části spektra je silně absorbována i část spektra pod hranou. Takto lze například pomocí Ni filtru odstranit „tvrdší“ Kb čáru mědi a ponechat „měkčí“ dublet Ka. Absorpční koeficienty pro různé prvky a jejich závislost na vlnové délce jsou tabelovány např. v [3].
V oboru rtg. záření lze index lomu n vyjádřit vztahem [4]
|
n = 1 - d - ib, |
(5) |
|
d = reNl2 /2p a b = ml/4p , |
(6) |
re = 2.818 x 10-15m je klasický poloměr elektronu a N je počet elektronů v jednotkovém objemu refraktující látky. Tzv. dekrement indexu lomu d nabývá v rtg. oboru hodnot řádově 10-5 – 10-6. Člen b souvisí s absorpcí a nebudeme ho zde uvažovat.
Jelikož je index lomu menší než jedna, paprsky se lámou od kolmice a za určitých podmínek dochází k totální reflexi. Ze Snellova zákona platí pro mezný úhel totální reflexe yc vztah cosyc = 1 - d. (Úhly měříme mezi dopadajícím paprskem a reflektujícím povrchem.) Vzhledem k velikosti d platí
|
(7) |
a s využitím (6)
|
(8) |
Úhly yc jsou poměrně malé, pro l = 0.15 nm s jejich velikost pohybuje v desítkách úhlových minut. K totální reflexi rtg. záření pak dochází pro úhly y, pro které platí 0 < y < yc . Koeficient reflexe (poměr intenzit odraženého a dopadajícího záření) se v tomto intervalu rovná jedné a pro y > yc prudce klesá. Vezmeme –li v úvahu i absorpci, pak koeficient reflexe pozvolna klesá i v intervalu 0 < y < yc (obr. 2 ). Podmínkou dobré reflektivity je však dokonale vyleštěný povrch reflektující látky - zrcadla.
Vymezíme-li svazek monochromatizovaného záření tak, že svírá s povrchem zrcadla jistý úhel, pak s dostatečnou intenzitou se budou reflektovat pouze ty paprsky, pro něž je mezný úhel totální reflexe větší, než tento úhel. Jinými slovy, dostatečně reflektovat se budou pouze ty paprsky, jejichž vlnová délka bude větší než hodnota odpovídající nastavenému úhlu podle vztahu (8). Do zrcadla naopak vstupuje záření o vlnových délkách kratších. Zrcadlo tak odstraňuje tvrdou část záření a kromě toho má roli optického elementu, podobně jako v optice viditelného záření. U stanic synchrotronového záření se často používá k odstraňování vyšších harmonických, které, jak bude ukázáno později, kontaminují monochromatizované záření u krystalových monochromátorů. U rentgenových lamp k odstranění harmonických zpravidla stačí snížit napětí na lampě.
Kombinace zrcadla a absorpčního filtru tak umožňuje předem vymezit určitý obor vlnových délek. Měkčí záření (větší l) se odstraní absorpčním filtrem a tvrdší (kratší l) zrcadlem.
Obr. 2
Závislost reflektivity při totální
reflexi na úhlu y.
Vhodný obor vlnových délek lze principielně vymezit i pomocí dvou zrcadel tak, že záření prošlé prvním tenkým zrcadlem a jehož spektrum je omezeno shora, se reflektuje od druhého zrcadla, které omezuje spektrum zdola. Pokusy o využití takovéto kombinace byly však zcela ojedinělé.
Zhruba je možné říci, že funkce krystalových monochromátorů je založena na využití Braggova zákona
|
2d sinq = kl, |
(9) |
kde d je mezirovinná vzdálenost difraktujících rovin, q je úhel, který svírá paprsek s difraktujícími krystalografickými rovinami, l je vlnová délka a k (celé číslo) je řád difrakce. Vymezíme-li tedy svazek záření tak, že dopadá na krystal pod úhlem q, krystal si z dopadajícího záření vybere vlnové délky (2d sinq)/k, kde k = 1, 2, … . Tyto vlnové délky nazýváme harmonickými, přičemž při k = 1 hovoříme o základní či první harmonické (fundamental harmonic) a při ostatních k hovoříme o vyšších harmonických. Někdy píšeme Braggův zákon ve tvaru
|
2(d/k) sinq = l. |
(10) |
Jestliže například difraktují roviny (111) a difrakce je ve třetím řádu, pak mluvíme o difrakci na rovinách (333), kde d333 = (d111)/3 . Pro některé harmonické platí, že strukturní faktor je nulový a taková harmonická pak neexistuje.
Orientace difraktujících rovin vzhledem k povrchu krystalu může být buď taková, že dopadající i difraktovaný paprsek leží v tomtéž poloprostoru vymezeném povrchem krystalu, pak mluvíme o Braggově difrakci, nebo taková, že difraktovaný paprsek vstupuje do krystalu, prochází jím a vychází na opačné straně krystalu a pak mluvíme o Laueho difrakci. Rovina difrakce je rovina určená dopadajícím paprskem a normálou k difraktujícím rovinám.
Rozlišujeme tyto základní typy Braggovy a Laueho difrakce:
Braggova symetrická – povrch rovnoběžný s difraktujícími rovinami,
Braggova asymetrická – povrch svírá jistý úhel s difraktujícími rovinami, normála k povrchu leží v rovině difrakce,
Braggova kosá (inclined) – povrch svírá jistý úhel s difraktujícími rovinami, normála k povrchu neleží v rovině difrakce a rovina určená normálou k difraktujícím rovinám a normálou k povrchu je kolmá k rovině difrakce,
Braggova obecně asymetrická - (kombinace předcházejících dvou),
Laueho symetrická – difraktující roviny jsou kolmé k povrchu,
Laueho asymetrická – difraktující roviny nejsou kolmé k povrchu.
 |
|
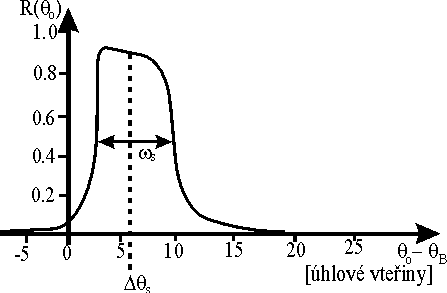
Obr. 3 |
K hlubšímu porozumění funkce krystalových monochromátorů jsou nutné znalosti základů dynamické teorie difrakce rentgenového záření na dokonalých krystalech [5, 6, 7, 8]. Její výklad však přesahuje rámec této kapitoly a proto se zde omezím pouze na prezentaci základních výsledků pro nejčastěji používané případy.
Braggův zákon dává pro určité l ostrou hodnotu q. Ukazuje se však, že tomu tak přesně není. Za prvé, skutečné q je poněkud větší než spočítané podle Braggova zákona a za druhé, k difrakci dochází v malém, ale konečném intervalu w. Závislost reflexního koeficientu C na q pro symetrickou Braggovu difrakci je ukázána na obr. 3. Z obrázku je vidět typicky asymetrický tvar křivky, který souvisí s nenulovým absorpčním koeficientem. Tato křivka se nazývá Darwinova-Prinsova funkce a u nás je též vžitý výraz krystalová funkce.
Šířka reflexního oboru (krystalové funkce) ws a odchylka Dqs jeho středu od qB , tj. úhlu q spočítaného z Braggova zákona pro určitou l jsou určeny vztahy:
|
ws = (2 rel2 P IFhrI e-M)/ pVsin2θB |
(11) |
|
Dqs = re l2 F0r / pVsin2θB, |
(12) |
Zde V je objem elementární buňky
(unit-cell), re = e2/mc2, Fhr
je reálná část strukturního faktoru Fh (h zde
zastupuje Műllerovy indexy hkl), P je polarizační faktor, a e-M
je teplotní faktor. Index s znamená,
že se jedná o symetrickou difrakci. Je li elektrický vektor kolmý na rovinu
difrakce, pak je P = 1. Leží-li však elektrický vektor v rovině
difrakce, pak P = cos 2q,
což znamená, že pro q
= 450 k difrakci nedochází.
Jak ws , tak i Dqs jsou velice malé, řádově v úhlových vteřinách. Například pro difrakci záření o vlnové délce l = 0.15 nm na rovinách (111) křemíkového monokrystalu, Si(111), je ws = 3.24 x 10-5 a Dqs = 3.04 x 10-5 . Z geometrického hlediska se krystal s povrchem rovnoběžným s difraktujícími rovinami chová jako zrcadlo. Úhel dopadu a úhel odrazu jsou stejné.
Z (11) a (12) je též vidět, že pro vyšší harmonické (kratší l a menší Fhr) jsou jak ws , tak i Dqs menší než pro základní harmonickou. Vyšší harmonické se tedy nedifraktují přesně pod stejným úhlem q jako základní harmonická. Přesně řečeno, pod stejným úhlem se difraktují vyšší harmonické odpovídající poněkud větší vlnové délce (větší qB).
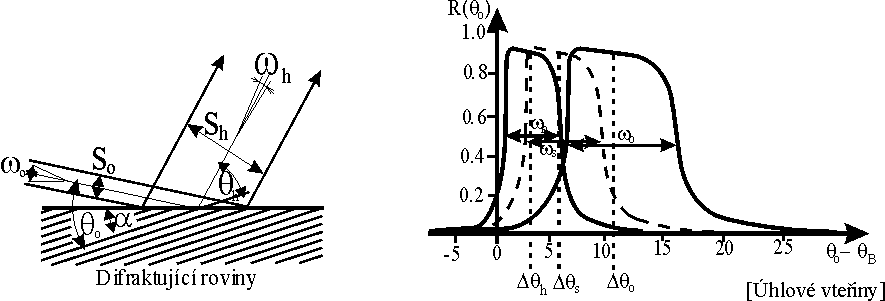
Obr. 4
Chod paprsků a Darwinovy-Prinsovy křivky
pro Braggovu asymetrickou difrakci.
Přejděme nyní k Braggově asymetrickému případu difrakce(obr. 4 ). Zde již difrakční obrazy paprsků o určité vlnové délce na straně dopadu a na straně odrazu nejsou symetrické a to nejen vzhledem k povrchu, což je evidentní, ale i vzhledem k difraktujícím rovinám. Tedy šířka úhlového oboru w0 a odchylka Dq0 jeho středu od Braggova úhlu qB pro paprsky „přijmuté krystalem k difrakci“ se liší od šířky úhlového oboru wh a odchylky Dqh jeho středu od qB pro difraktované paprsky. Mezi těmito veličinami platí následující vztahy:
|
w0
= ws
b-1/2 , Dq0 = (1/2) (1+1/b) Dqs , wh
= ws (b)1/2,
Dqh = (1/2) (1+b) Dqs , θ0
= θB + Dq0,
θh =
θB + Dqh , b = sin (θB – α) / sin (θB + α).
|
(13) |
b je tzv. index asymetrie, který se rovná jedné pro symetrický případ (a = 0). (Často se ale používá poněkud odlišná definice b, která dává hodnotu –1 pro symetrickou difrakci). Úhel α je úhel mezi difraktujícími rovinami a povrchem a je brán jako kladný když dopadající paprsek svírá s povrchem menší úhel než difraktovaný. Pro průřezy S0 a Sh difraktovaného paprsku na straně dopadu a odrazu platí
|
Sh = S0 / b, |
(14) |
a spolu s (13)
|
wh Sh = w0 S0. |
(15) |
Veličiny w a Dq představují zpřesnění Braggova zákona, které je důsledkem refrakce. Jestliže je asymetrie například taková, že se na straně dopadu w a Dq zmenšují (a < 0, b > 1), pak na straně výstupu se w a Dq zvětšují. Průřez vystupujícího (difraktovaného) svazku je menší než průřez svazku dopadajícího.
Zde se dosud předpokládalo, že na
krystal dopadá divergentní monochromatický svazek. Přímým důsledkem výše
popsaného je , že i když na „asymetrický“ krystal dopadá paralelní
polychromatický paprsek, pak difraktovaný paprsek je poněkud odchýlený od
zrcadlově odraženého paprsku a má
též malou divergenci. Tento jev lze též považovat za projev refrakce
při asymetrické difrakci. Pro stanovení rozlišovací schopnosti
monochromátoru je důležité vědět, jaký interval vlnových délek Dl
projde monochromátorem i přesto, že dopadající
svazek je přesně paralelní. Zřejmě platí, že
|
Dl = w0 /D = w0 (dl/dq) = w0 (2d/k) cosq, |
(16) |
kde D je disperze spočítaná z Braggova zákona.
Braggova kosá difrakce se chová jako
symetrická v tom smyslu, že w0
= ws.
Divergence difraktovaného svazku má však složku do směru kolmého na rovinu
difrakce a tato složka je tím větší, čím větší je „kosost“
difrakce. (Složka divergence do roviny difrakce je opět ws.)
Dopadá-li na takovýto krystal paralelní polychromatický svazek, pak
difraktovaný svazek je lehce odkloněn ve směru kolmém na rovinu difrakce
(sagitálním směru) a má též malou sagitální divergenci, což je projevem
refrakce při kosé difrakci.
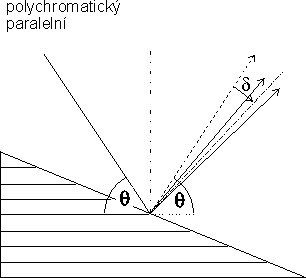
Interval vlnových délek, který monochromátorem prochází, je stejný jako u
symetrické difrakce. Oba případy
jsou schematicky znázorněny na obr. 5
(odchylky difraktovaného paprsku a jeho
divergence jsou pro názornost silně přehnané).
 |
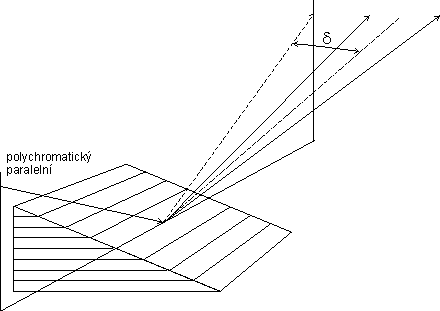 |
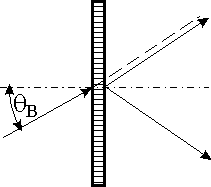
| Obr. 5 Odchylky a divergence difraktovaného svazku pro dopadající paralelní a polychromatický svazek záření. Nalevo je asymetrická difrakce, napravo je kosá difrakce. |
|
 |
|
Obr. 6 |
Laueho symetrická difrakce se vyznačuje tím, že difraktovaný paprsek vstupuje do krystalu, prostupuje krystalem a na výstupním povrchu se štěpí na dva paprsky: jeden má směr dopadajícího paprsku a druhý směr paprsku odraženého na difraktujících rovinách (obr. 6). Difrakce se i zde řídí Braggovým zákonem. I zde platí, že šířka difrakčního úhlového oboru (krystalové funkce) pro monochromatické záření je konečná, a zužuje se pro vyšší harmonické. Na rozdíl od Braggova případu je krystalová funkce symetrická a pro všechny harmonické je centrovaná na Braggově úhlu qB.
U Laueho asymetrického případu difrakci rovněž popisuje Braggův zákon, avšak v detailech je situace složitější a nebudeme se jí zde zabývat.
U jednokrystalového monochromátoru vymezujeme štěrbinou určitý interval úhlů q, čímž vymezujeme i určitý interval vlnových délek. Vynikající pomůckou k ilustraci funkce krystalových monochromátorů jsou DuMondovy diagramy vyložené např. v [4],[8], kde je rovněž popsána většina monochromátorů uvedených v tomto textu.
DuMondův diagram pro jednokrystalový monochromátor a symetrickou difrakci je v podstatě grafické zobrazení Braggova zákona se zahrnutím refrakčních jevů podle dynamické teorie tak, jak bylo ukázáno výše (obr. 7). Vzhledem k tomu, že difrakce není ostrá ale dochází k ní v určitém intervalu ws, zobrazí se v diagramu nikoliv ostrá sinusoida ale tenký pás, poněkud posunutý vzhledem k sinusoidě 2d sinq doprava o Dqs.
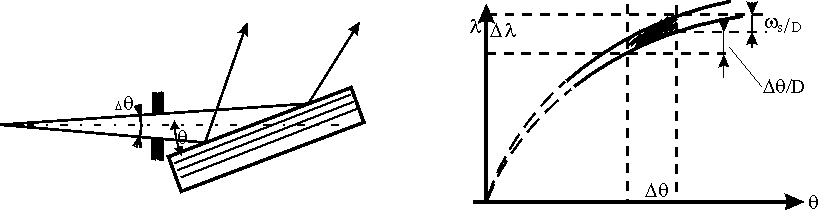
Obr. 7
Z DuMondova graffu na obr. 7 vidíme, že vymezíme-li jistou divergenci svazku Dq, monochromátor propustí obor vlnových délek Dl , kde
|
Dl = ws / D + Dq / D. |
(17) |
Odsud je vidět, že i když bychom dovedli zařídit, aby dopadající svazek záření byl dokonale paralelní, pak Dl neklesne na nulu, nýbrž na hodnotu ws / D. Jinými slovy, rozlišovací schopnost jednokrystalového monochromátoru je omezena shora hodnotou
|
Ri = Dl/ws, |
(19) |
což je tzv. vnitřní (intrinsic) rozlišovací schopnost. Tu lze zvýšit pouze použitím vyššího řádu difrakce, pro který je ws menší, a nebo použitím asymetrické difrakce tak, aby w0 < ws . V tomto případě asymetrické difrakce vystupující svazek zúžíme. Jestliže, naopak, nám jde více o intenzitu než o rozlišení, pak volíme asymetrii tak, aby w0 > ws . V tomto případě vystupující svazek rozšíříme. DuMondův diagram se pro asymetrickou difrakci a jednu harmonickou skládá ze dvou překládajících se nebo dokonce oddělených pásů o různých šířkách (w0, wh).
Je třeba si však uvědomit, že při vymezení určité divergence dopadajícího záření se difraktují také vyšší harmonické. Ty v případě jednokrystalového monochromátoru můžeme odstranit pouze snížením napětí na rtg. lampě nebo použitím zrcadla, a nebo je prostě neregistrovat pomocí amplitudového analyzátoru pulzů tam, kde je to možné.
Z Braggova zákona plyne omezení vlnových délek, pro které je možno použít monokrystalů jakožto monochromátorů. Omezení shora je jednoznačné; maximální l je dána maximální možnou hodnotou q = 900, z které plyne
|
lmax = 2d |
(20) |
Tak například pro nejdokonalejší krystaly, jimiž jsou krystaly křemíku, platí d111 = 0.313 nm, a tudíž lmax = 0.62 nm. Existují však i jiné, méně dokonalé krystaly, pro které je lmax větší, jako např beryl (1.59 nm) nebo slída (1.98 nm) a existuje řada organických krystalů, pro které je lmax ještě větší. Omezení zdola je spíše technického rázu. Je-li q velikosti jednoho či několika stupňů, pak začínají vzrůstat nároky na rozměr krystalu a přesnost úhlového nastavení. Úhel q lze zvýšit zvýšením řádu difrakce; toto zvýšení je však zase na úkor intenzity.
Jak bylo uvedeno výše, jedna složka Dl (17) souvisí s divergencí svazku záření Dq dopadajícího na krystal. Tuto složku při existujícím Dq lze eliminovat pouze tehdy, bude-li se dhkl laterálně měnit tak, že součin dhkl(q) sinq bude konstantní. Takovéto krystaly (graded crystals) byly připraveny a úspěšně vyzkoušeny v BESSY (nový zdroj synchrotronového záření v Berlíně). Jde o krystaly křemíku dopované germaniem tak, že se koncentrace Ge laterálně mění. Vzhledem k malé divergenci synchrotronového záření se koncentrace Ge mění jen málo. Typický koncentrační gradient je 0.8%/cm. Podobného efektu lze dosáhnout i s normálním krystalem tak, že se z divergentního, na krystal dopadajícího svazku vytvoří zrcadlem (např. parabolickým) svazek paralelní.
Laueův krystalový monochromátor (tj. monochromátor založený na Laueho difrakci) se v zásadě chová podobně jako Braggův monochromátor. I zde vymezujeme jisté Dq k docílení monochromatizace. Intenzita monochromatizovaného záření je však podstatně menší než u Braggova krystalu. To je dáno jednak tím, že se uvnitř krystalu generuje více vlnových polí, z nichž některé se v důsledku vysoké absorpce absorbují ještě v krystalu. Dále tím, že vystupující záření se ještě rozštěpí na dvě složky, z nichž pouze jedna je použita. Tyto krystaly se používají hlavně pro monochromatizaci tvrdého záření (krátké l) a to ze dvou důvodů. První důvod je ten, že pro krátké l je absorpce malá a ztráty intenzity nejsou příliš velké a dále malé q nevyžadují velké rozměry krystalu, neboť záření dopadá na povrch krystalu téměř kolmo. Určitou výhodou Laueho krystalu je to, že při dostatečné tloušťce krystalu je difraktované záření polarizované v celém rozsahu q.
Dosud jsme diskutovali divergenci dopadajícího záření v rovině difrakce, tedy tzv. meridionální divergenci Dq. Záření ale má také divergenci Df ve směru kolmém na rovinu difrakce (sagitální divergenci). Lze dokázat, že jestliže se určitý paprsek dopadající na krystal s Braggovým úhlem q difraktuje s vlnovou délkou l, pak paprsek od něj odkloněný ve směru kolmém na rovinu difrakce o úhel f se difraktuje s vlnovou délkou
|
lf = l cosf |
(21) |
Z toho plyne: bude-li mít dopadající svazek sagitální divergenci f, pak difraktované záření bude obsahovat vlnové délky v intervalu od l cos(f/2) do l, přičemž spektrální intenzita v tomto intervalu roste směrem k l. Z (21) je zřejmé, že na rozdíl od meridionální divergence, sagitální divergence ovlivňuje hodnotu Dl až když je f dostatečně velké.
V tomto uspořádání jsou dva stejné krystaly nastaveny do paralelní polohy tak, že všechny paprsky, které se difraktují od prvního krystalu se difraktují také od druhého krystalu (obr. 8.). Při difrakci na prvním krystalu je difraktovaný paprsek pootočen vzhledem k dopadajícímu v jednom smyslu, a při difrakci na druhém krystalu dojde k pootočení v opačném smyslu. Odtud označení (+,-). Podobně jako u jednokrystalového monochromátoru, se interval propouštěných vlnových délek určuje nastavením q a velikosti štěrbiny. „Krystalová funkce“ tohoto uspořádání je součinem C2 krystalových funkcí. Na rozlišovací schopnost má toto uspořádání vliv jen do té míry, že funkce C2 má mohem nižší postranní hodnoty (tails) než funkce C a tedy monochromatizace je „čistší“, neboli lépe omezena na interval, kde se krystalová funkce zřetelně odlišuje od nuly. Vlnová délka se ladí otáčením obou krystalů jako celku. Hlavní předností tohoto uspořádání je to, že difraktovaný paprsek od druhého krystalu postupuje ve stejném směru jako paprsek dopadající na první krystal. To je nesmírně důležité při monochromatizaci synchrotronového záření, kde aparatura se vzorkem má své stabilní místo.
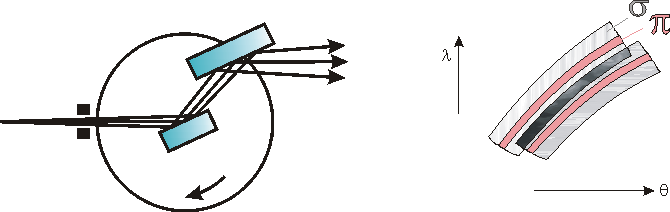
Obr. 8
Dvoukrystalový monochromátor v (+,-)
bezdisperzním uspořádání a DuMondův diagram.
DuMondův diagram pro toto uspořádání se skládá z grafu pro první krystal, což je pás, jak jsme uvedli dříve, a grafu pro druhý krystal. Ten znázorňuje reflektivitu druhého krystalu, ale v závislosti na úhlu q, s kterým paprsky dopadají na první krystal. Tedy i zde je grafem pás. Jsou-li oba krystaly nastaveny přesně do paralelní polohy, pak se oba pásy přesně překrývají a vše, co se difraktuje od prvého krystalu se difraktuje i od druhého. Jestliže nyní oba krystaly poněkud rozladíme z paralelní polohy, například pootočením druhého krystalu o úhel Dq kolem osy kolmé na rovinu difrakce, pak pás odpovídající druhému krystalu se posune o Dq ve směru osy q vzhledem k pásu odpovídajícímu prvnímu krystalu. K difrakci nyní dochází pro ta q a l , která odpovídají překryvu obou pásů. Tento překryv je ale stejný pro všechny hodnoty q (obr. 8). Při dalším pootočení krystalu dochází k současnému vymizení překryvu pro všechna q a monochromátorem již neprochází žádné záření. Otáčením pouze jednoho (druhého) krystalu tedy nemůžeme nastavovat vlnovou délku, jako tomu je u jiných uspořádání, a proto se toto uspořádání nazývá bezdisperzní. Představme si nyní do DuMondova grafu pro paralelní uspořádání (symetrickou difrakci) zakresleny pásy i pro vyšší harmonické a rovněž zvlášť pro s a p polarizační komponentu. Je zřejmé, že slabým rozjustováním lze dosáhnout několika efektů.
Mírné zvýšení vnitřní rozlišovací schopnosti, neboť překrývající se část pásů je užší než šířka každého pásu. „Krystalová funkce“ tohoto uspořádání je dána funkcí C(q)C(q-Dq). Při větším rozjustování klesá maximální hodnota této funkce natolik, že její pološířka naopak roste.
Jelikož šířky pásů pro vyšší harmonické jsou vždy menší než šířka pásu pro základní harmonickou, dojde při určitém rozjustování k tomu, že se již nepřekrývají pásy pro vyšší harmonické při ještě dostatečném překryvu pásů pro základní harmonickou. Při tomto rozjustování tedy toto krystalové uspořádání propouští část základní harmonické a potlačuje podstatně vyšší harmonické.
Jak plyne z dřívějšího výkladu, je šířka pásu pro p polarizační komponentu cos2q násobek šířky pásu pro s polarizační komponentu, tedy je užší. Podobně jako v předcházejícím bodu rozjustováním můžeme značně omezit překryv pásů pro p komponentu při ještě dostatečném překryvu pásů pro s komponentu (obr. 8). Jinými slovy, toto uspořádání funguje jako polarizátor, a to i pro úhly q odlišné od 450.
Obtížnost tohoto uspořádání spočívá v tom, že oba krystaly musí být sjustovány s vysokou přesností, i na zlomky úhlové vteřiny. Jakákoliv nestabilnost aparatury či okolní teploty se může projevit v prudkém samovolném poklesu intenzity. V ideálním případě by měly osy otáčení obou krystalů být rovnoběžné a s nimi by měly být rovnoběžné i příslušné difraktující roviny. Pak při dostatečné sagitální divergenci má reflexe za druhým krystalem tvar čáry nebo pásu. Tato reflexe se při pootočení jednoho krystalu naráz objeví či zmizí, a to jako celek. Jestliže jsou ale difraktující roviny skloněny vůči ose otáčení, pak je obraz reflexe menší a při meridionálním otáčení jednoho z krystalů (tj. kolem osy kolmé na rovinu difrakce) se pohybuje ve směru kolmém na rovinu difrakce. Tento obraz zkušený experimentátor využívá k sjustování sklonu obou krystalů.
Jestliže tedy máme sjustované sklony
obou krystalů, pak při postupném otáčení např. druhého krystalu kolem
osy kolmé na rovinu difrakce a registrací difraktovaného výkonu dostáváme
tzv. rocking curve (RC), která je konvolucí dvou krystalových funkcí:
|
RC(Dq) = ∫C(x)C(x-Dq)dx, |
(22) |
kde x = q - qB . Jedním z kriterií dokonalosti monokrystalů pro jejich použití jako rentgenových monochromátorů je to, že difraktují podle dynamické teorie, čili že jejich krystalová funkce má tvar teoretické Darwin-Prinsovy funkce. Tuto funkci je ale obtížné přímo změřit. Je však poměrně snadné spočítat konvoluci krystalových funkcí (22) a porovnat ji s naměřenou křivkou. Zatím co funkce C je silně asymetrická, RC je vždy symetrická.
Při proměřování RC si musíme uvědomit, že současně měříme křivky pro různé polarizační komponenty a pro různé harmonické, přičemž se šířky těchto křivek navzájem liší. U synchrotronového záření, které je lineárně polarizované, se vyšší harmonické projevují jako úzký pík superponovaný na širší křivce základní harmonické. Je pak poměrně snadné nastavit krystaly mimo tento pík a tak se zbavit vyšších harmonických.
I když vystupující svazek pokračuje ve směru dopadajícího paprsku, přesto se se změnou q posouvá. Aby se zajistila fixní poloha monochromatického svazku, musí se se změnou q také vhodně měnit vzdálenost krystalů. Takto pracuje většina monochromátorů synchrotronového záření.
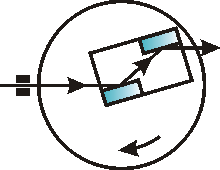 |
| Obr. 9 Žlábkový (channel-cut) monochromátor. |
Problém udržení stability justáže obou krystalů lze jednoduše odstranit tak, že se obě difrakční plochy vyrobí do jednoho monokrystalu (obr. 9). Vznikne jakýsi žlábek, kde k difrakci dochází na vnitřních stěnách tohoto žlábku (channel-cut crystal). Výhodou je „přirozená“ sjustovanost obou difraktujících částí a to, že monochromatizovaný svazek záření pokračuje ve směru dopadajícího. Nicméně, v této jednoduché formě má takovýto monochromátor i některé nevýhody. Vystupující svazek se při změně q posouvá, nelze odstranit harmonické slabým rozjustováním, a nelze korigovat zahřátí první difrakční plochy pootočením druhého krystalu. Dále, dopadá-li na takovýto krystal polychromatické synchrotronové záření, pak dochází k difrakci paprsků různých vlnových délek na různých krystalografických rovinách. Tyto paprsky se difraktují na první difraktující části krystalu do různých směrů, avšak druhá difraktující část je vrátí opět do směru difrakce hlavního paprsku, tj. do směru dopadajícího záření. Tyto parazitní reflexe (tzv. glitches) je někdy velice obtížné odlišit od hledané reflexe. Pokud se používá dvou oddělených krystalů, pravděpodobnost vzniku těchto parazitních reflexí je menší, a pokud se objeví, stačí jeden z krystalů pootočit kolem normály k difrakčním rovinám.
 |
|
Obr. 10 |
Přirozená sjustovanost obou difrakčních ploch u channel-cut monochromátoru je takovou předností, že se hledaly cesty, jak výše uvedené nevýhody odstranit.
Parazitní reflexe u channel-cut monochromátoru zcela odstranit nelze; lze ale zvolit takovou orientaci řezů, pro kterou je počet těchto reflexí minimální.
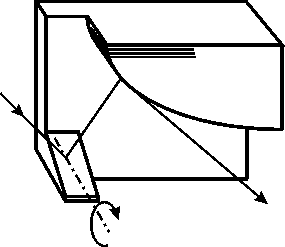
Pokud jde o harmonické, jsou možné dva přístupy. Jedním přístupem je naříznout channel-cut krystal tak, aby bylo možno elastickou deformací obě difrakční plochy navzájem slabě rozjustovat. Druhý přístup spočívá v asymetrických řezech obou difrakčních ploch tak, že se indexy asymetrie na obou plochách vhodně liší. Tím dojde k vzájemnému posunu krystalových funkcí tak, že se již funkce pro vyšší harmonické nepřekrývají při ještě dostatečném překryvu funkcí pro první harmonickou. Aby toto platilo v širokém rozsahu Braggových úhlů, musí se index(y) asymetrie s q předem určeným způsobem měnit, čili musí být alespoň jedna difrakční plocha vhodně zakřivená. Ukazuje se, že tato plocha musí mít exponenciální tvar [9] (obr. 10).
Problém fixní polohy difraktovaného svazku se dá u channel-cut krystalu rovněž řešit několika způsoby. Jedním způsobem je opět vhodné zakřivení difrakčních ploch. Posunutí vystupujícího paprsku totiž závisí na vzdálenosti konkrétních difraktujících krystalografických rovin na obou difraktujících částech krystalu a na Braggově úhlu. Aby poloha vystupujícího svazku byla fixní, nezávislá na q, musí se tato vzdálenost s q měnit. Jiný způsob jak tuto vzdálenost měnit je využít asymetrické difrakce na jedné difraktující části a posunu krystalu ve směru kolmém na osu otáčení krystalu a nebo využít kosou difrakci na jedné části a pohybu krystalu ve směru osy otáčení. Channel-cut krystal, který by měl první difraktující část říznutou tak, že difrakce je kosá a druhou difrakční část zakřivenou do exponenciálního tvaru by odstraňoval harmonické v celém rozsahu úhlů q a současně by umožňoval fixní polohu monochromatického svazku [9] (obr. 10). Nastavení úhlu q zde musí být doprovázeno translací jednak ve směru osy otáčení a jednak i ve směru na ní kolmém.
|
|
Dosud jsme mluvili o takovém (+,-) uspořádání, kde na obou krystalech (či částech krystalu) dochází k Braggově difrakci. Zvláštním případem monolitického (+,-) uspořádání je případ, kdy na prvním krystalu dochází k Laueho difrakci a na druhém k Braggově difrakci (obr. 11). Z toho, co jsme řekli o obou typech difrakce plyne, že k tomu, aby obě difraktující části difraktovaly současně, je třeba nepatrně deformovat Laueho část. Tím dojde k překryvu funkcí pro první harmonickou, nikoliv však pro vyšší harmonické. Lze rovněž ukázat, že při změně nastavení Braggova úhlu otáčením monochromátoru kolem styčné přímky obou jeho difraktujících částí zůstává poloha vystupujícího svazku konstantní. Navíc zde dochází k tzv. polychromatické fokusaci. |
Toto uspořádání se používá poměrně vzácně (u nás se též objevil název neparalelní uspořádání). Připomíná bezdisperzní uspořádání s tím, že oba krystaly jsou podobné, nikoliv stejné. Typickým uspořádáním je např. kombinace Si a Ge krystalů difraktujících na rovinách stejného typu. DuMondův diagram se pak skládá ze dvou pásů majících sice stejné znaménko směrnice ale sklon pásů je pro každý krystal jiný. Znamená to, že se pásy protínají i když jedním z krystalů pootáčíme v širokém rozsahu úhlů. Průnik obou pásů vymezuje vlnový a úhlový obor který prochází monochromátorem. Tyto obory jsou poměrně široké a jsou vymezeny krystalovým uspořádáním bez nutnosti použití štěrbin a závisejí na vzájemném natočení krystalů. Systém tedy má disperzi vzhledem k úhlovému nastavení jednoho z krystalů. Není to tedy již tak, jako u bezdisperzního uspořádání, kdy se difraktuje vše a nebo nic. Rovněž vyšší harmonické se difraktují v širokém rozmezí úhlů otáčení jednoho z krystalů a nelze zde aplikovat nějaké rozladění jako v bezdisperzním případě. Na druhé straně však, vzhledem k různosti krystalů, průsečíky pásů pro jednotlivé harmonické odpovídají nepatrně odlišným úhlům q a je zde tedy principielní možnost oddělit vyšší harmonické štěrbinou.
Jelikož směrnice obou pásů se příliš neliší, pootočení jednoho z krystalů vede k rychlému posunu průsečíku (průniku) obou pásů, čili disperze monochromátoru je malá; odtud název slabě disperzní.
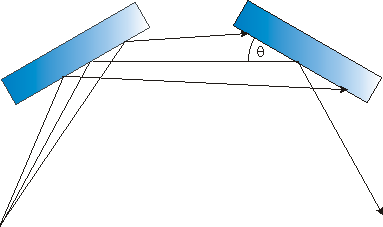
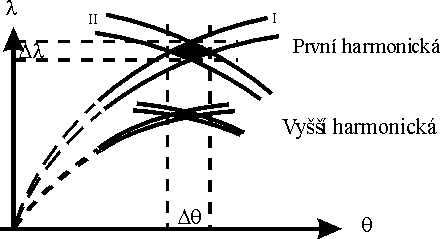
Disperzní (+,+) uspořádání je patrné na obr. 12. Zpravidla se používá dvojice stejných krystalů. Předpokládejme, že jistý paprsek se od obou krystalů difraktuje se stejným q. Potom jiný paprsek, který se od prvního krystalu difraktuje s menším úhlem, dopadá na druhý krystal naopak s větším úhlem a tam pro něj není proto splněna Braggova podmínka a tudíž se nedifraktuje. Podobně je tomu pro paprsky, které se od prvního krystalu difraktují s úhlem větším. Pásy v DuMondově diagramu jsou orientovány tak, že směrnice mají opačná znaménka (obr. 13). Pásy se protínají, a to pro všechny úhly q. Na rozdíl od předcházejícího odstavce však průnik odpovídá pouze úzkému oboru q a l. Takovýto monochromátor bez pomoci štěrbin propouští velice malý úhlový (meridionální) a vlnový obor, a to i tehdy, je-li zdroj záření široký. Rozlišovací schopnost se tedy prakticky rovná vnitřní rozlišovací schopnosti. Ze symetrie DuMondova grafu pro stejné krystaly je zřejmé, že se všechny harmonické difraktují do jednoho úhlu a toto uspořádání tudíž neumožňuje odstranění vyšších harmonických.
 |
 |
|
Obr. 12 |
Obr. 13 |
Dosud jsme mlčky uvažovali pouze o meridionální divergenci svazku. V případě velké sagitální divergence leží pro každý bod zdroje všechny paprsky difraktované druhým krystalem v rovině rovnoběžné s průsečnicí difraktujících rovin obou krystalů. Pro tyto paprsky přitom platí (21). Tento vztah umožňuje zobrazení spektra v režimu tzv. vertikální disperze. Zpravidla se však sagitální divergence omezuje a l se ladí otáčením druhého krystalu kolem osy kolmé k rovině difrakce. Dá se snadno ukázat, že disperze je pak dvojnásobkem disperze spočítané z Braggova zákona.
Toto uspořádání (obr. 14 ) v sobě spojuje výhody obou předcházejících a používá se hlavně pro synchrotronové záření (i když ne příliš často) . Hlavní výhody jsou vysoká rozlišovací schopnost, fixní poloha vystupujícího svazku a možnost odstranit vyšší harmonické rozladěním jednoho z párů paralelních krystalů. U synchrotronového záření se ladí vlnová délka současným otáčením obou (+,-) párů proti sobě. V tomto případě je disperze taková, jaká vychází z Braggova zákona.
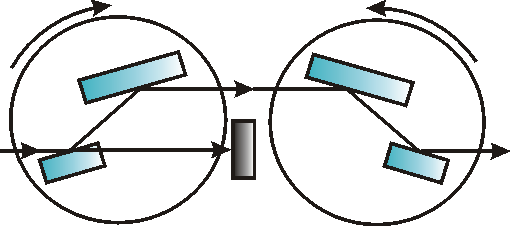
Obr. 14
Aby byla difrakce kvalitní, musí být difraktující povrch krystalů kvalitní. Po vyříznutí a mechanickém opracování povrchu krystalů zůstane povrchová vrstva tlustá několik nm, která má silně narušenou krystalovou strukturu. Tato vrstva značně narušuje kvalitu difrakce. K odstranění této vrstvy je nutno povrch krystalů oleptat. Leptací proces však není zcela rovnoměrný a výsledkem může být struktura povrchu, která připomíná kůru pomeranče. Takovýto povrch může mít rovněž negativní vliv na kvalitu difrakce, zvláště při silně asymetrické difrakci. Proto se např. u krystalů křemíku osvědčuje tzv. mechanicko-chemické leštění, které dává hladký a lesklý povrch, který je přitom i krystalicky dokonalý.
Multivrstva je jakýsi umělý krystal, který vznikne střídavou depozicí vrstev lehkého (A) a těžkého (B) prvku na vhodný substrát [10, 11]. Vznikne tak periodická struktura s periodou d, která je součtem tloušťek vrstev lehkého (dA) a těžkého (I) prvku (obr. 15). I pro takovouto strukturu platí Braggův zákon podobně jako u krystalů. Rozlišovací schopnost je však podstatně horší. Pro vnitřní rozlišovací schopnost platí, že
|
l/Dl = N, |
( 23) |
kde N je počet period přispívajících k interferenci. Typické hodnoty rozlišovací schopnosti jsou 10 – 200. Perioda d bývá v rozmezí od 1.5 nm do několika desítek nm. Jako materiálu A se např. používá uhlíku, křemíku, berylia nebo bóru, kdežto materiálem B bývá např. wolfram nebo platina.
|
|
|
Obr. 15 |
Multivrstvy mají oproti krystalům výhodu v tom, že je lze deponovat na libovolně tvarovaný povrch a tím snadno docílit fokusace monochromatizovaného záření (zatímco krystaly je nutno ohýbat). Další výhodou je to, že hodnotu d lze měnit jak laterálně, tak i do hloubky. Laterální změnou d docilujeme stejného efektu, jaký byl popsán u graded krystalů. Takovéto multivrstvy se nazývají Göbelovo zrcadlo. Změnou d do hloubky lze docílit značného rozšíření difrakční křivky a tím vytvoření tzv. superzrcadla. Multivrsvy se hodí tam, kde jde o intenzitu a ne o rozlišovací schopnost. Díky široké difrakční křivce a relativně dobré stabilitě některých moderních multivrstev se tyto také používají k premonochromatizaci.
Při použití rovinných monochromátorů se z veškerého záření emitovaného zdrojem využívá jen malá část. Proto se za účelem lepšího využití záření zdroje a tudíž zvýšení difraktované intenzity využívá fokusačních metod.
 |
|
Obr. 16 |
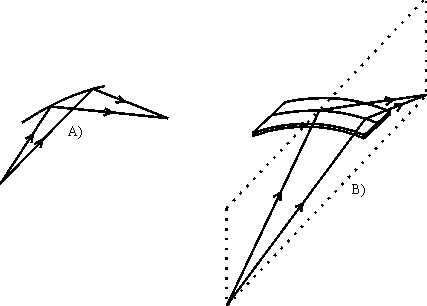
Monochromatizované záření je možno fokusovat pomocí zrcadla, což činí aparaturu složitější, i když zde je současně možnost odstranění vyšších harmonických zrcadlem. Druhá možnost je docílit fokusace vhodným ohnutím či tvarováním krystalů a právě toto bude předmětem této kapitoly. Není zde přitom místo na popis všech možných uspořádání; omezíme se spíš jen na základní věci. Připomeňme znovu, že rovinou difrakce rozumíme rovinu, obsahující normálu k difraktujícím krystalografickým rovinám (v místě dopadu paprsku) a dopadající paprsek. Dopadá-li na krystal divergentní svazek záření v rovině difrakce pro střední paprsek, pak fokusaci paprsků v této rovině difrakce nazýváme fokusací meridionální. Leží-li však dopadající paprsky v rovině kolmé na rovinu difrakce středního paprsku, pak fokusaci těchto paprsků nazýváme fokusací sagitální. Oba typy fokusací jsou znázorněny na obr. 16. Záměrně se vyhýbám výrazům horizontální a vertikální fokusace, což v klasické rtg. laboratoři kde rovina difrakce je horizontální, odpovídá meridionální a sagitální fokusaci. U synchrotronového záření je tomu totiž naopak a může dojít k nedorozumění.
Jestliže je fokusace taková, že se sice paprsky fokusují z různých úhlů ale s různou vlnovou délkou, pak mluvíme o fokusaci polychromatické, na rozdíl od fokusace monochromatické, kde se z různých úhlů fokusují paprsky o stejné vlnové délce. Oba typy mají svůj význam.
Funkce některých fokusujících monochromátorů je založena na vlastnostech elipsy. Pro každý bod elipsy platí, že tečna v tomto bodě svírá stejný úhel s průvodiči elipsy, tj. spojnicemi tohoto bodu s ohnisky elipsy. To znamená, že máme-li zrcadlo ve tvaru elipsy, pak každý paprsek který vychází z jednoho ohniska elipsy se po odrazu na zrcadle vrací do druhého ohniska. Dále pro elipsu obecně platí, že součet délek obou průvodičů je pro všechny body elipsy stejný. Ke každým dvěma ohniskům je možno vytvořit nekonečně mnoho elips.
Rozlišovací schopnost fokusačních monochromátorů je zpravidla o něco horší než u metod s rovinnými krystaly. Faktory, které ji určují, jsou podobné jako u rovinných krystalů a navíc zde přistupuje ještě optická vada vlastní metody (aberace), vliv odchylek od ideálního tvaru, hloubka pronikání záření do krystalů, atd. Diskuse těchto faktorů je někdy komplikovaná a nebudeme se jí zabývat. Účinnou metodou pro vyšetřování fokusačních vlastností je zde metoda ray-tracing.
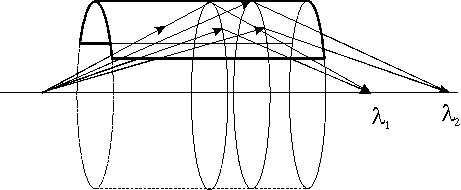
Jestliže je krystal ohnut do tvaru válce a bodový zdroj záření je na jeho ose, pak paprsky difraktované s jistým q či l tvoří kuželovou plochu a difraktují se tak, že se fokusují do jednoho místa na této ose, přičemž vzdálenost zdroje od krystalu je stejná jako vzdálenost krystalu od fokusu. Jedná se tedy o optickou soustavu, pro kterou je zvětšení 1 : 1. Tato metoda fokusace se nazývá metoda Von Hamosova. Má-li dopadající paprsek divergenci v obou směrech, pak se do různých míst na ose válce fokusují paprsky o různých vlnových délkách (obr 17). Jedná se tedy o fokusaci monochromatickou. Tato metoda byla např. použita jako spektrometru pro diagnostiku plasmatu.
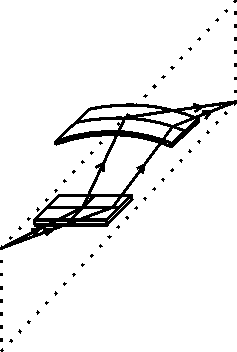
U stanic synchrotronového záření se velice často pro sagitální fokusaci používá dvoukrystalová (+,-) modifikace této metody . Synchrotronové záření má poměrně malou vertikální divergenci a vertikální rozměr svazku je též malý. Horizontální divergence může však být podstatně větší a proto se horizontální fokusaci zpravidla přikládá větší význam. Vzhledem k tomu, že u monochromátorů pro synchrotronové záření je rovina difrakce vždy vertikální, je horizontální fokusace vždy fokusací sagitální. Sagitálně fokusující (+,-) monochromátor je ukázán na obr. 18 . Zde je třeba si uvědomit, že monochromátorem projdou pouze ty paprsky, pro které je současně splněna Braggova podmínka na obou krystalech. Pokud bychom předpokládali nulovou šířku krystalové funkce, pak by tyto paprsky byly dva pro rozladěný monochromátor (paprsky by byly symetricky uspořádané vzhledem k rovině difrakce) a tyto paprsky by se slily v jeden pro sjustovaný monochromátor. Díky konečné šířce krystalové funkce může být úhlová oblast ve které dochází k fokusaci dostatečná. Zdánlivý zdroj (zrcadlový obraz zdroje vzhledem k prvnímu rovinnému krystalu) přitom nemusí ležet na ose válce. Existuje však jeden případ, kdy se všechny paprsky, které se difraktují od prvního krystalu, difraktují také od druhého krystalu. To nastává tehdy, když zdánlivý zdroj leží na protilehlé stěně válce. V tomto případě je zvětšení optické soustavy, přesněji zmenšení, 3 : 1. Fokusace je zde opět monochromatická, je maximálně efektivní co do difraktované intenzity, ale pokud jde geometrickou kvalitu fokusace, není dokonalá. Znamená to, že záření z bodového zdroje se nefokusuje do bodu ale do plošky.
 |
 |
|
Obr. 17 |
Obr. 18 |
Ohneme-li krystal do tvaru elipsy, pak všechny paprsky vycházející z jednoho ohniska se fokusují do druhého ohniska. Různé paprsky však mají různá q, a tedy i l. Extrémním případem elipsy je parabola. Krystal ohnutý do parabolického tvaru fokusuje rovnoběžný svazek záření do bodového ohniska. V těchto případech se jedná o fokusaci polychromatickou (přitom se často eliptický či parabolický tvar aproximuje tvarem válcovým). Z ohniska pak vychází divergentní paprsek s určitou úhlovou disperzí (vlnová délka závisí jistým způsobem na úhlu). Toho se využívá při spektroskopické metodě nazývané disperzní EXAFS.
 |
|
Obr. 19 |
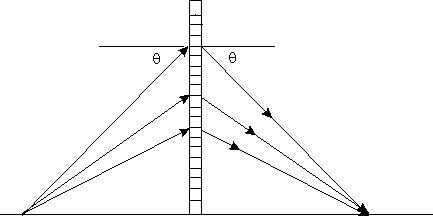
U Laueho difrakce existuje polychromatická fokusace pro jednu větev difraktovaného záření dokonce i u neohnutého krystalu, jak ukazuje obr. 19. V tomto případě je poměr vzdáleností zdroj–krystal a krystal-fokus 1 : 1. Lze ukázat, že jiného poměru lze dosáhnout ohnutím krystalu do hyperbolického tvaru.
Vymezením určitého intervalu Dq vymezíme určité Dl a záření o tomto rozmezí vlnových délek je fokusováno.
Existují dvě cesty, jak alespoň v Braggově případě změnit polychromatickou fokusaci na fokusaci monochromatickou. Jednou z cest je použít graded krystaly, nebo Göbelova zrcadla v případě multivrstev. Mezirovinnou vzdálenost je nutno laterálně měnit tak, aby se pro každý paprsek difraktovala vždy stejná vlnová délka. Tento způsob se skutečně používá.
Druhá cesta je komplikovanější. Představme si, že do elipticky ohnutého krystalu vyfrézujeme válcový profil tak, že jak zdroj, tak i fokus, tedy obě ohniska elipsy, leží na stěnách válce. Každé místo na takovémto povrchu difraktuje paprsky vycházející z jednoho ohniska elipsy do jejího druhého ohniska, neboť difraktují krystalografické roviny ohnuté do tvaru elipsy. Současně ale pro kružnici platí matematická věta o obvodovém a středovém úhlu; totiž že všechny obvodové úhly nad tětivou (spojnicí obou ohnisek) jsou stejné. Z toho plyne, že se všechny paprsky difraktují se stejným q a tedy i stejným l. Jedná se tedy o monochromatickou meridionální fokusaci, což je základní idea Johanssonovy metody. Rozeberme tento problém podrobněji (obr. 20 ). Na tomto obrázku je síť elips, reprezentující difraktující krystalografické roviny. Krystal v poloze A představuje symetricky difraktující ohnutý krystal, v němž je vyroben válcový profil s poloměrem R. Krystal v poloze B je asymetricky difraktující krystal se středním úhlem asymetrie w, je rovněž ohnutý a je do něj také vyroben profil o poloměru R. Je zřejmé, že přímky A1P, A2P, B1P a B2P jsou normály k difraktujícím rovinám na povrchu válcového povrchu. Normála totiž musí půlit úhel mezi paprskem dopadajícím a difraktovaným (odhlédneme-li od malých refrakčních efektů popsaných dříve). Aby tedy byly úhly mezi normálou a dopadajícím paprskem a normálou a difraktovaným paprskem (což jsou obvodové úhly nad oblouky F1P a PF2 ) stejné, pak i příslušné oblouky musí být stejné, což v případě bodu P jsou. Odtud je ihned vidět, že poloměr zakřivení krystalu A je PA1 nebo PA2, což je právě 2R. Všechny paprsky, a to od obou krystalů, jsou difraktovány se stejným q a tudíž i stejným l. Kružnice na obrázku se nazývá Rowlandovou kružnicí a krystal A představuje Johanssonovu metodu fokusace. Jestliže nyní posuneme zdroj záření z bodu F1 do E1, pak se všechny paprsky o určité, ale větší vlnové délce než v předcházejícím případě budou difraktovat do symetricky položeného bodu E2, tedy odlišného od F2. Toto plyne opět z rovnosti oblouků E1P a PE2 a rovnosti všech obvodových úhlů nad těmito oblouky.
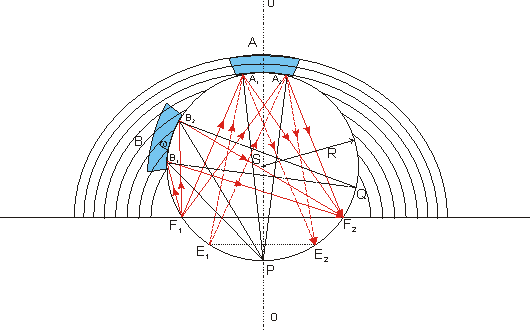
Obr. 20
Princip polychromatické a monochromatické
fokusace na bázi ohnutých krystalů.
|
|
|
Obr. 21 |
Nyní můžeme odhlédnout od sítě elips a shrnout naše poznatky takto: symetricky difraktující krystal ohneme tak, aby měl poloměr křivosti 2R, vyrobíme do něj válcový profil o poloměru R a umístíme ho na Rowlandovu kružnici o poloměru R tak, že jeho povrch bude ležet na této kružnici. Leží-li na Rowlandově kružnici bodový zdroj záření, pak se v závislosti na jeho umístění budou od krystalu difraktovat pouze paprsky o určité vlnové délce a tyto paprsky se budou opět fokusovat na Rowlandovu kružnici, a to tak, že vzdálenosti zdroj krystal a krystal fokus budou přibližně stejné. Jestliže nyní umístíme na Rowlandovu kružnici a nebo někam mezi ohnisko F1 a krystal plošný zdroj záření, pak každý bod zdroje na Rowlandově kružnici (ať již reálný nebo virtuální) bude zářit do určitého bodu na opačné straně kružnice s jistou vlnovou délkou, která je však pro každý bod jiná. Jinými slovy, přiložíme li na Rowlandovu kružnici rtg. film, dostaneme na něm zobrazeno spektrum zdroje. Na tomto principu funguje Johanssonův spektrometr.
Lze ukázat, že i když do krystalu nevytvoříme válcový profil a pouze krystal ohneme tak, aby měl poloměr 2R, pak fokusace již nebude přesně monochromatická ale odchylka od přesné monochromatičnosti bude přijatelně malá. Takovéto uspořádání se nazývá Johannovo (obr. 21).
Vraťme se však ke krystalu B. Otázka je, jaký musí být poloměr křivosti ohnutí asymetricky difraktujícího krystalu. Víme, že normály k difraktujícím rovinám v bodech B1 a B2 se protínají v bodu P. Normály k povrchu v bodech B1 a B2 (před vyrobením válcového profilu) musí svírat stejný úhel jako normály k difraktujícím krystalografickým rovinám a tudíž jejich průsečnice musí také ležet na Rowlandově kružnici. Na obr. 20 se jedná o bod Q. Čili i zde vidíme, že poloměr zakřivení je 2R. Na rozdíl od krystalu A jsou vzdálenosti zdroj krystal a krystal fokus různé. Z předcházejícího víme, že úhel PBQ = w. Dále úhly F1BP = PBF2 = p/2 - q. Potom úhel F2BQ = w-p/2+q a F1BQ = w+p/2-q. Nyní je zřejmé, že p = BF1 = 2R cos(F1BQ) a q = BF2 = 2R cos(F2BQ). Z těchto vztahů přímo plyne
|
p = 2R sin (q - w), q = 2R sin (q + w), |
( 24) |
a
|
p/q = sin (q
- w) / sin (q
+ w), |
což je tzv. Guinierova fokusační podmínka.
Z této základní konstrukce je již možno bez velkých problémů odvodit i některá další uspořádání, jako například metodu Cauchoisové (obr. 22 ), která používá Laueho difrakci. Jedna se o analogii metody Johanna. Krystal je ohnut podobným způsobem, pouze difraktující roviny jsou k povrchu kolmé. Zdroj záření musí být plošný a monochromátor si pro fokusaci vybírá konvergentní svazek. Podobně analogií Johanssonova monochromátoru (spektrometru) pro Laueho difrakci je DuMondův – Kirpatrickův monochromátor (spektrometr).
Metody Johanna, Johanssona, Cauchoisové i
DuMonda-Kirpatricka, lze odvodit, jak bylo ukázáno, z polychromatické
fokusace. Avšak symetricky difraktující krystal je možno také ohnout tak,
že všechny paprsky vycházející z bodového zdroje se diffraktují se
stejným úhlem q
a tedy i se stejnou vlnovou délkou l.
Křivka, podle které musí být krystal ohnut, je tzv. logaritmická spirála, kterou lze v polárních souřadnicích
popsat výrazem
|
r = exp( pf). |
( 25) |
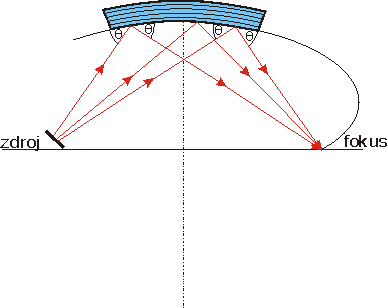
Fokusace není v tomto případě dokonalá, ohniskem je ploška. Obrátíme-li však chod paprsků (obr. 23 ), pak se monochromatické záření z plošného zdroje bude fokusovat do bodu. Zde se tedy jedná o čistou meridionální monochromatickou fokusaci.
|
|
 |
|
Obr. 22 |
Obr. 23 |
Logickým vyústěním snahy o maximální výstupní intenzitu je kombinace meridionální a sagitální fokusace, tj. použití krystalu s dvojí křivostí ve dvou navzájem kolmých směrech [12]. V tomto případě jsou však příslušné křivosti na sobě závislé.
Monochromátory, resp. spektrometry s ohnutými krystaly, existují v převážné většině jako jednokrystalové. Existují však i metody, založené na kombinaci rovinného a zakřiveného krystalu, např. [13] nebo dvou zakřivených krystalů, např [14]. Těmito metodami se zde zabývat nebudeme.
4.4
Fokusující monochromátory na principu difrakčně-refrakční optiky.
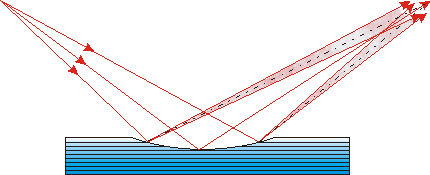
Krystaly mohou sagitálně i meridionálně fokusovat, aniž by bylo nutno je ohýbat, využijeme-li refrakčních jevů při difrakci, popsaných v odstavci 3.1.[15]. Vyrobíme-li do krystalu transversální drážku (s osou kolmou na rovinu difrakce) vhodného tvaru, pak dno drážky difraktuje symetricky a boční stěny difraktují asymetricky. Přitomm dochází vlivem refrakce k vychýlení difraktovaného paprsku tak, že dochází k meridionální fokusaci. Fokus však není ostrý vlivem chromatické aberace. Zde se jedná o polychromatickou fokusaci (obr. 24 ).
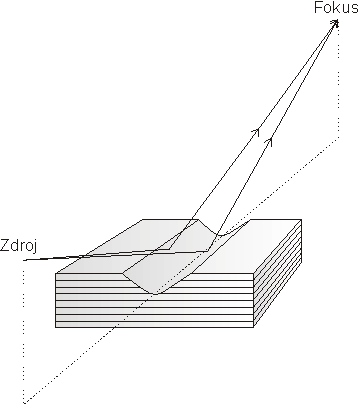
Vyrobíme-li do krystalu podélnou (parabolickou) drážku, pak difrakce na stěnách drážky je kosá a difraktované paprsky jsou vlivem refrakce odchýleny sagitálně tak, že dochází k sagitální fokusaci (obr. 25). Lze ukázat, že je výhodné disperzní uspořádání (+,-) krystalů takové, že drážka je na obou krystalech. Jednak se tím kompenzuje rozšíření svazku v rovině difrakce, ke kterému dochází po difrakci na jedné drážce a jednak se tím docílí kompenzace sagitálního rozšíření fokusu, který může být proto ostrý. Vzhledem k tomu, že difrakčně refrakční jevy jsou malé, je tato metoda vhodná pouze pro fokusaci úzkých svazků na delší vzdálenost, tedy zejména k fokusaci synchrotronového záření. Tam je pak vhodné uspořádání čtyřkrystalové (+,-,-,+), nejlépe s podélnými drážkami na všech čtyřech krystalech . Výroba takovýchto krystalů však není jednoduchá. Naštěstí je možné s dostatečnou přesností aproximovat parabolickou drážku cylindrickou drážkou a dva krystaly s drážkami v (+,-) uspořádání realizovat ve formě kruhového otvoru vyrobeného do jednoho monokrystalu. Takovýto monochromátor se pak skládá ze dvou krystalů s kruhovým otvorem nastavených do disperzní polohy ( obr. 26 ). Záření se pak v každém krystalu difraktuje dvakrát na vnitřní straně kruhového otvoru. Vyrobíme-li drážku či otvor tak, že jejich osa není rovnoběžná s difraktujícími rovinami, docílíme tím zkrácení fokusační vzdálenosti a přibližně konstantní polohy fokusu v širokém oboru vlnových délek.
 |
 |
|
Obr. 24 |
Obr. 25 |
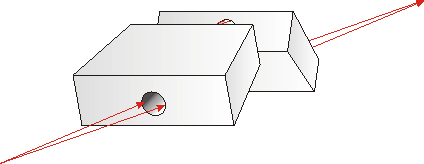
Obr. 26.
Sagitálně fokusující
(+,-,-,+) monochromátor. Záření se difraktuje uvnitř podélných kruhových děr.
Parametry synchrotronového záření se v mnohem liší od záření z rentgenových lamp. Tomu se musí přizpůsobit i monochromátory. Jejich provedení se tak odlišuje od monochromátorů v klasických rentgenových laboratořích.
Synchrotronové záření je lineárně polarizované tak, že elektrický vektor leží v horizontální rovině. Proto jsou krystaly vždy uspořádány tak, že rovina difrakce je vertikální, aby se vyloučil polarizační faktor cos2q. Jak již bylo uvedeno dříve, zejména z důvodů geometrických, používají se krystaly v paralelním uspořádání, aby vystupující paprsek měl stejný směr jako paprsek dopadající. Synchrotronové záření však v některých případech může být kruhově polarizované, a pak je zapotřebí, aby monochromátor tento stav polarizace nenarušil. Pokud je q malé, pak se obě polarizační složky difraktují se zhruba stejnou intenzitou. Pro velká q se někdy používá zkříženého uspořádání, které vznikne z paralelního uspořádání tak, že se druhý krystal pootočí kolem dopadajícího paprsku o 900. Pak se s polarizační složka na prvním krystalu stane p složkou na druhém krystalu a p složka na prvém krystalu se stane s složkou na druhém krystalu. Výsledek je ten, že jsou obě polarizační složky potlačeny stejně a vystupující záření zůstává kruhově polarizované.
Z dynamické teorie difrakce plyne existence dvojlomu v krystalech při difrakci. V krystalu se šíří pro každou polarizační složku vlny s poněkud odlišným vlnovým vektorem, čili s různou fázovou rychlostí. Při určité tloušťce krystalu (řádově jednotek až desítek mikrometrů) dochází ke vzniku fázového posunu p/2 . To platí jak pro Laueho difrakci, tak i pro lehce rozladěnou Braggovu difrakci ( q poněkud mimo oblast hlavní reflexe). Dopadá-li potom na krystal lineárně polarizované záření a je.li krystal vhodně natočen, pak je difraktované záření (v Braggově případu prošlé záření) nejen monochromatické, ale i kruhově polarizované. Toto je čtvrtvlnná destička v rentgenovém oboru. Její funkce byla prvně demonstrovaná s rtg. lampou a později byla používaná se synchrotronovým zářením.
Synchrotronové záření ze zdrojů 3. generace má vysoký stupeň koherence, což znamená, že povrchy krystalů musí být velice kvalitní, aby se koherence zachovala i po monochromatizaci. Ukázalo se, že například asymetrická difrakce není vhodná pro zachování koherence a zřejmě to platí i pro kosou difrakci.
Synchrotronové záření, zejména záření z undulátorů, má tvar tenkých svazků o průřezu 1-2 mm2, které je třeba fokusovat na velkou vzdálenost, např. 5 – 10 m. V některých případech se vyžaduje velikost fokusu řádově v mikronech, i menší. To klade značné nároky na přesnost zhotovení optických elementů, včetně monochromátorů, která musí být podstatně větší než v klasických laboratořích. Zde se uplatňuje jedna z výhod difrakčně-refrakční optiky, neboť k malému vychýlení difraktovaného paprsku je třeba velké odchylky povrchu od difraktujících rovin a nároky na přesnost tvaru difraktujícího povrchu nejsou tedy zdaleka takové jako například u sagitálně ohnutého krystalu.
Největším problémem je však velký výkon ve svazcích synchrotronového záření, který u wiglerů dosahuje hodnot několika kW a vysoká hustota výkonu záření, která u undulátorů dosahuje desítek až stovek W/mm2. Tyto hodnoty by vedly k rychlé destrukci monochromátoru, pokud by nebyla učiněna vhodná opatření. K destrukci nejen že nesmí dojít, ale funkce monochromátoru musí zůstat zachovaná i za těchto podmínek. Znamená to, že deformace vyvolané tepelnými gradienty musejí být minimální. Je několik způsobů, jak čelit této vysoké tepelné zátěži.
Téměř vždy je třeba první krystal chladit. U záření z ohybových magnetů stačí tzv. nepřímé chlazení, kdy je 1-2 mm tlustý Si monokrystal pomocí Ga-In eutektika spojen s měděnou deskou, kterou proudí chladící voda. U záření z wiglerů je již třeba vyrobit chladící kanálky přímo do Si krystalu, a to až asi 1 mm pod pracovní povrch; je to tzv. přímé chlazení, technicky velice obtížně realizovatelné, má-li mít monochromátor požadované parametry.
Rozšířené (ale současně i velice drahé) je kryogenní nepřímé (začíná se i s přímým) chlazení prvního krystalu. Křemík má totiž v blízkosti teploty kapalného dusíku nulový koeficient tepelné roztažnosti. Znamená to, že teplotní gradienty vyvolávají jen minimální deformační gradienty. Tepelná vodivost je při těchto teplotách rovněž větší.
Jiným přístupem užívaným u undulátorů je použití málo absorbujících krystalů. Záření, které se nedifraktuje, projde s minimální absorpcí krystalem a nezpůsobuje tudíž velké teplotní gradienty. Takovými krystaly jsou krystaly diamantu. Navíc je zde možnost kryogenního chlazení, neboť diamant má při teplotách kapalného dusíku podobné vlastnosti jako křemík. Nevýhodou je, že současná technologie umožňuje připravit krystaly poměrně malých rozměrů a proto se diamantové krystaly pro záření z wiglerů zatím neužívají.
Podobně jako málo absorbující krystaly by se měly chovat velice tenké krystaly. Platí totiž, že extinkční hloubka je vždy menší než absorpční hloubka. K difrakci přispívá hlavně povrchová vrstva krystalu o tloušťce rovné extinkční hloubce. Část krystalu pod touto vrstvou již k difrakci příliš nepřispívá, způsobuje ale ohřátí krystalu díky absorpci. Z toho plyne idea této metody: použít krystal o tloušťce extinkční hloubky. Problém zde ale je, že tak tenký krystal se snadno deformuje a proto je realizace této metody velice obtížná.
Snížení hustoty dopadajícího výkonu záření lze docílit použitím asymetrické nebo kosé difrakce. Tím se dopadající paprsek rozprostře na velkou plochu krystalu, ale současně se tím zvětší průřez difraktovaného paprsku. Proto musí mít druhý krystal povrch rovnoběžný s prvním, aby se průřez svazku dostal do původních rozměrů. Asymetrická difrakce je zde méně výhodná, protože omezuje obor laditelnosti úhlů q.
Deformace způsobené zahřátím lze také do jisté míry kompenzovat mechanicky na principech adaptivní optiky. Lze také přizpůsobovat změnám prvního krystalu tvar druhého krystalu.
Výše uvedené metody je možné kombinovat. Tyto metody omezení tepelných účinků SZ fungují u současných zdrojů synchrotronového záření jako je např. ESRF v Grenoblu, avšak bez velké rezervy.
Zdroje SZ čtvrté generace jsou lasery na volných elektronech. Zatím jsou ve stádiu konstrukce. Rentgenový zdroj čtvrté generace TESLA se buduje v Německu. Záření z těchto zdrojů bude mít o několik řádů vyšší spektrální brilianci než má záření z undulátorů v ESRF. Bude plně koherentní. Záření bude mít pulsní charakter, přičemž délka pulsů se bude pohybovat v desítkách či stovkách fs.
To, co bylo řečeno o monochromátorech pro zdroje synchrotronového záření třetí generace, platí i zde. Pokud jde o problémy s tepelnou zátěží, je zřejmé, že situace zde bude ještě kritičtější, než je tomu u současných zdrojů třetí generace, a proto v tomto směru probíhá intenzivní výzkum. Hlavní charakteristikou zdrojů čtvrté generace je ale krátkost pulsů, která umožní studovat procesy, nezachytitelné předchozími zdroji. Je proto nutné, aby optika, zejména monochromátory, zachovaly tuto charakteristiku záření i po monochromatizaci [16].
Předpokládejme, že pomocí ohnutého krystalu chceme fokusovat svazek záření. Pokud budou optické dráhy jednotlivých paprsků různé, pak budou do ohniska přicházet jednotlivé pulsy postupně a dojde tak k rozšíření výsledného pulsu. Odtud plyne výhoda eliptického ohnutí, neboť u elipsy je součet průvodičů konstantní.
Problém ovšem je i u jednoduchého krystalu. Předpokládejme, že máme nekonečně krátký puls, který dopadá na krystal. Dále předpokládejme, že se tento puls zanořuje do krystalu až do extinkční hloubky. Po celou dobu průchodu krystalem je tento puls rozptylován atomy krystalu a tedy difraktované záření bude tvořeno pulsem, jehož délka odpovídá řádově extinkční hloubce krystalu. Tedy nekonečně krátký puls byl difrakcí transformován na puls konečné délky. Puls o reálné délce trvání 100 fs odpovídá délce 30 mm a to je již hodnota, která se blíží hodnotám extinkčních hloubek dokonalých krystalů (jako např. Si nebo diamant) které se pohybují v jednotkách mm. Takovýto puls bude již difrakcí na prvním krystalu pozorovatelně rozšířen a k dalšímu rozšíření ještě dojde při difrakci na druhém krystalu. Nejde přitom jen o rozšíření pulsu při difrakci; mění se zřejmě i charakter difrakce samé. Když puls záření dorazí k povrchu krystalu, pouze malé množství atomů se zúčastní rozptylu a ten by měl být více méně Thomsonovský, čili do všech směrů. Tak jak se puls bude zanořovat do krystalu, počet atomů podílejících se na rozptylu poroste a difrakce bude mít postupně charakter dynamické difrakce.
Chování monochromátorů při difrakci takto krátkých intensivních pulsů se studuje teoreticky a všechny modely jsou zatím na úrovni spekulací. Jisté však je, že u zdrojů SZ čtvrté generace vyvstává problém zachování tvaru a délky pulsů generovaných zdrojem, zejména u pulsů krátkých (desítek a jednotek fs). Je tedy zřejmé, že bude třeba vyloučit kinematicky difraktující krystaly, neboť jejich extinkční hloubka je podstatně větší než u krystalů dokonalých. I mezi dokonalými krystaly však jsou rozdíly. Poměrně malou extinkční hloubku mají např. krystaly diamantu.
Ch. G. Dood, Handbook of X-Rays, red. E. F. Kaelble, kap. 5. Mc.Graw Hill 1967.
Z. Johan, R. Rotter a E. Slánský, Analýza látek rentgenovými paprsky, SNTL 1970.
H. J. Milledge,
International Tables for X-Ray Crystallography, sv.III, red.
C. H. MacGillavry
a G. D. Rieck, str. 175, D. Reidel Publ. Comp. 1983.
R. Caciuffo, S.
Melone, F. Rustichelli, A. Boeuf, Phys. Reports 152,
č.1,
(1987), 1.
W. Batterman, H.
Cole, Rev. Modern Physics, 36,
No.3,(1964), 681-717.
A. Authier,
Dynamical Theory of X-Ray Diffraction, Oxford university press Inc. New
York, 2001.
V. Valvoda, M.
Polcarová, P. Lukáč, Základy strukturní analýzy, Universita Karlova
1992.
T. Matsushita, H.
Hashisume, Handbook on Synchrotron Radiation, sv. 1A,
red. E. E. Koch, kap. 4, North-Holland 1983.
J. Hrdý,
Czech J. Phys. B 40, No.3, (1990), 361-366.
P. Chakraborty,
Int. J. Modern Physics B5, č.3,
(1991), 2133.
B. W. Batterman,
D. H. Bilderback, Handbook on Synchrotron Radiation,
red. G. S. Brown a D. E. Moncton, North-Holland 1991, Vol. 3,
kap. 4, str. 105.
D. B. Wittry a D.
M. Golijanin, Appl. Phys. Lett. 52,
4.17, (1988), 1381.
B. W. Batterman a
L. Berman, Nucl. Instrum. Methods 208,
(1983),327.
K. Tohji a Y. Udagawa, Rev. Sci. Instr. 59, č.7, (1988), 1127.
J. Hrdý, N. Artemiev, A. K. Freund a J. Quintana, Diffractive-Reffractive Optics for Focusing Hard X-Rays Beams, Proceeding SPIE Vol. 4501, San Diego, 29 July 2001, 88 – 98.
Proceedings SPIE, svazek 4500, Optics for Fourth-Generation X-Ray Sources, SPIE 2001.