Podmínkou pro difrakci rentgenového záření o vlnové délce λ na osnově rovin s difrakčními indexy hkl a mezirovinnou vzdáleností dhkl je, aby záření dopadalo na tyto roviny pod úhlem θhkl, který splňuje Braggovu rovnici
V případě monokrystalu je možné tuto podmínku splnit vhodnou orientací krystalu
vzhledem k dopadajícímu svazku záření.
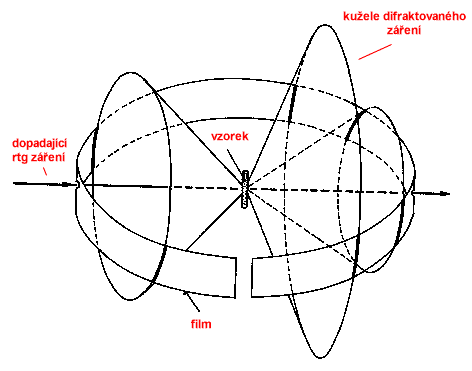
V případě polykrystalického nebo práškového vzorku s náhodnou orientací jednotlivých krystalových zrn je pravděpodobné, že některá zrna budou orientována tak, že zmíněné roviny (hkl) budou právě v difrakční poloze. Tato pravděpodobnost bude tím větší, čím větší bude počet zrn v ozářeném objemu. Záření difraktované rovinami. (hkl) jednoho zrna se bude dále šířit ve směru, který svírá úhel 2θhkl se směrem dopadajícího záření. Kdybychom natáčeli uvažované krystalové zrno kolem osy totožné s normálou difraktujících rovin, zůstávaly by roviny (hkl) stále v difrakční poloze (neboť stále svírají úhel θhkl s dopadajícím svazkem) a difraktované paprsky by se posouvaly po ploše kužele s vrcholovým úhlem 4θhkl a s osou ležící ve směru dopadajícího záření. Po této kuželové ploše se budou šířit i difraktované paprsky od všech zrn, jejichž roviny (hkl) jsou právě v difrakční poloze.
Zatím jsme diskutovali pouze jedinou osnovu rovin. Vezmeme-li v úvahu všechny další osnovy rovin, jejichž mezirovinné vzdálenosti spolu s danou vlnovou délkou rentgenového záření mohou splňovat difrakční podmínku, dostaneme jako výsledný difrakční jev soustavu kuželových ploch s osami podél dopadajícího záření a s vrcholovými úhly 4θ, danými mezirovinnými vzdálenostmi rovin. Je tedy zřejmé, že měřením difrakčních úhlů múžeme určit mezirovinné vzdálenosti.
| Nejjednodušší způsob je založen na filmovém záznamu difraktovaných paprsků na film uložený ve válcové komůrce, v jejímž středu se nachází vzorek. Geometrie vychází z obrázku. Práškový vzorek je nanesen na tenkou tyčinku, potaženou amorfní vrstvičkou lepidla. K vnitřním stěnám komůrky je přiložen film. Svazek rtg záření je vycloněn vstupní štěrbinou kruhového průřezu s průměrem většinou 0,5-1 mm. V dnešní době se konstruují i Debyeovy-Scherrerovy goniometry, kdy místo filmu se difrakční maxima registrují pomocí detektoru. Aby byly splněny podmínky Debyeovy-Scherrerovy metody, tj. velký počet náhodně orientovaných zrn v ozářeném objemu, je při malých rozměrech vzorku zapotřebí jemných prášků s rozměry zrn v oboru 10-5 -10-7m. Vzorek je třeba vycentrovat do středu (osy) komůrky (goniometru). Během expozice se vzorek otáčí kolem osy, neboť tím se zvyšuje pravděpodobnost postupného nastavení dalších krystalových zrn do reflexní polohy. |  |
Za konvenční práškovou difrakci lze v současnosti označit difraktometrii v Braggově-Brentanově parafokusačním uspořádání.
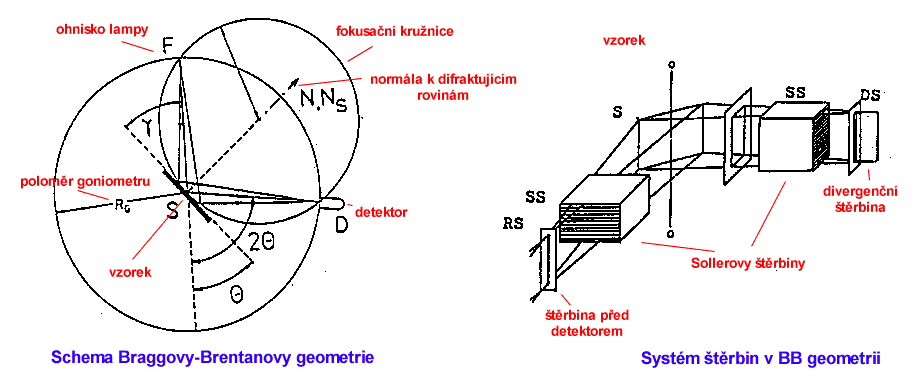
V tomto uspořádání je práškový vzorek natlačen do plochého držáku umístěného v ose goniometru. Snímání záznamu se provádí při pohybu detektoru rychlostí 2θ a pohybu vzorku rychlostí θ. Jedná se o případ symetrické difrakce, kdy úhel dopadu je stejný jako úhel odchodu. Registruje se tak vždy difrakce na rovinách hkl splňujících difrakční podmínku pro dané θ,které jsou orientovány rovnoběžně s povrchem vzorku. Znamená to, že pro různá hkl dostáváme informaci z různých zrn.
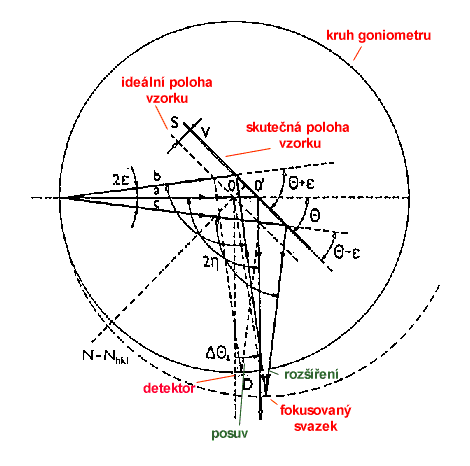
Ve všech difrakčních geometriích se projevují různé instrumentální chyby. V případě Braggovy-Brentanovy difrakce je nejvážnějším efektem vysunutí vzorku z osy. To vede jednak k posunu difrakční linie a jednak k jejímu rozmazání. Difraktovaný svazek se totiž fokusuje v jiném místě než je detektor. Z geometrického náčrtu lze odvodit funkční závislost posunu linií na difrakčním úhlu (~ cos θ/RG ). Tuto znalost lze využít při vyhodnocování mřížového parametru.
Dosud jsme předpokládali dopadající záření jediné vlnové délky. Získání monochromatického záření pomocí difrakce na krystalu-monochromátoru je spojeno s úbytkem intenzity v primárním svazku a proto se pro běžná měření nejčastěji využívá nejintenzivnějších složek charakteristického spektra použité rentgenové lampy: dubletu Kα1, Kα2. Rozdíl vlnových délek tohoto dubletu je natolik malý, že se projeví rozštěpením difrakcí pouze u vyšších difrakčních úhlů. To vyplývá přímo z Braggovy rovnice. Pokud je toto rozštěpení pozorováno, je při interpretaci zapotřebí používat příslušné vlnové délky jednotlivých složek dubletu. Nutno zdůraznit, že v tomto případě se jedná o dvě difrakce od téže osnovy rovin pro dvě různé vlnové délky, obsažené v dopadajícím svazku rentgenového záření. Kromě dvou nejintenzívnějších složek existují ve spektru rtg lampy další a nezanedbatelné je i spojité záření. Tyto komponenty se potlačují pomocí absorbčních filtrů či monochromátorů.
Volba rentgenové lampy, tj. vlnové délky se řídí druhem zkoumaného
materiálu. Je nežádoucí, aby dopadající záření budilo ve vzorku vlastní emisi
rtg záření, tzv. fluorescenční záření, které zvyšuje pozadí. Jeho vznik lze
očekávat v těch případech, kdy pro vlnové délky záření uvažované rtg lampy
nabývají absorpční koeficienty atomů studovaného materiálu vysokých hodnot.
Dále je obecně pro krystaly s nízkou symetrií nebo velkou jednotkovou buňkou typické
velké množství difrakčních linií. Jejich počet se sníží a vzájemná
vzdálenost zvětší, použijeme-li rentgenovou lampu s delší vlnovou délkou.
Nejčastěji používanou rentgenovou lampou je lampa s měděnou anodou, jejíž vlnová
délka složky Kα1 leží zhruba uprostřed
vlnových délek vyráběných lamp.
Složky charakteristického záření (v 10-10 m) |
||||
anoda |
Kα1 |
Kα2 |
Kα |
Kβ |
| Cu | 1.54050 | 1.54434 | 1.5418 | 1.39217 |
| Co | 1.78889 | 1.792801 | 1.79019 | 1.620703 |
| Mo | 0.70261 | 0.71354 | 0.706253 | 0.632253 |
Střední vlnová délka Kα se používá, není-li dublet rozlišitelný.
Metody rentgenové strukturní analýzy používající monokrystalické vzorky umožňují často úplné stanovení krystalografické charakteristiky krystalu. Při difrakci na monokrystalech získáváme totiž intenzity difrakcí od jednotlivých osnov krystalografických rovin, pro každou jejich orientaci zvlášť, a počet registrovaných maxim je velmi vysoký řádově 102-104. U práškové metody můžeme na debyegramu nebo difraktogramu rozlišit maximálně asi 100 linií. Navíc každá difrakční linie je superpozicí difrakcí od všech ekvivalentních i neekvivalentních rovin.
Je tedy zřejmé, že komplexní strukturní analýzu u krystalů se složitou
strukturou nebo nízkou symetrií lze úspěšně provádět pouze difrakcí na
monokrystalech. Převážná většina krystalických látek se však vyskytuje
v polykrystalické podobě a vypěstování monokrystalu je často obtížné. Navíc
práškové metody jsou nenahraditelné tam, kde rozhodující roli při určování
vlastností materiálu hraje právě jeho polykrystalická struktura (fázové složení,
velikost a orientace zrn, napětí apod. ).