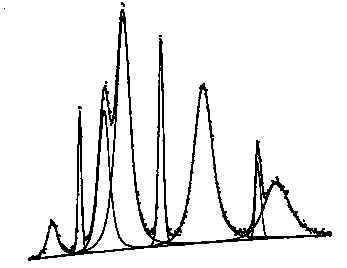

Práškový rentgenový difraktogram obsahuje řadu cenný údajů o mikrostruktuře zkoumaného materiálu. Jelikož je ovšem rentgenová difrakce, na rozdíl např. od elektronové mikroskopie, metodou nepřímou, není vždy jednoduché všechny obsažené informace dešifrovat. Prvním nezbytným krokem je co možno nejpřesnější určení parametrů naměřených difrakčních profilů jednotlivých difrakcí a dále korekce instrumentálních vlivů.
Profil rtg difrakční linie lze vyjádřit jako závislost měřené difraktované intenzity I, nejlépe v pulsech za jednotku času, na difrakčním úhlu θ resp. 2θ. Někdy je vhodné používat stupnici reciprokých mezirovinných vzdáleností (difrakčního vektoru) s = 2 sin θ/λ
Profil je možné charakterizovat několika parametry, které přímo souvisí s některými strukturními a mikrostrukturními charakteristikami materiálu, jak je uvedeno v následujícím schematickém přehledu.
Polohy difrakčních píků (θo) |
mřížové parametry - geometrie krystalové mříže - poruchy krystalové mříže, zbytková napětí |
| kvalitativní fázová analýza | |
Integrální intenzity (I) |
struktura krystalové mříže (strukturní motiv, druh atomů, ..) |
| ~ ozářenému objemu vhodně orientovaných krystalitů - přednostní orientace krystalitů, kvantitativní fázová analýza | |
| Debyeovy-Wallerovy faktory (střední kvadratické výchylky atomů) | |
Šířky |
velikost koherentně difraktujících oblastí - krystalitů |
| vnitřní nehomogenní mikroskopická napětí, poruchy krystalové mříže (dislokace, dislokační smyčky) | |
Tvarové parametry |
rozdělení poruch, velikostí částic, indikace typu poruch |
Polohy a intenzity lze při nepříliš vysokých nárocích na přesnost určovat i ze spojitých záznamů. Pro studium šířek a tvaru profilů je však třeba provést podrobnější analýzu a pro efektivní zpracování je samozřejmě nutné užít krokový záznam a digitální zpracování.
V současnosti existují asi tři skupiny metod zpracování difrakčních záznamů:
Přímá analýza |
předpokládá možnost správného určení pozadí, které je měřitelné na obou stranách profilu |
| 1. Separace pozadí | je komplikovanější při značně rozšířených profilech, kdy je tendence pozadí přecenit. I když ne všechny příspěvky k pozadí jsou lineární s difrakčním úhlem, často se aproximuje pozadí přímkou. Za oblst, ve které se měří, lze vzít takovou, kde ho je možné na obou stranách píku aproximovat stejnou lineární závislostí. |
| 2. Korekce na dublet | Při použití klasických zdrojů záření a
běžných práškových difraktometrů pracujeme vždy s dubletem Kα1,α2. Pro přesnou analýzu profilů a zvláště pro její správnou interpretaci je třeba provést separaci linie Kα2. Byla publikována řada postupů, z nichž většina je založena na třech předpokladech: profil složky Kα1 má stejný tvar jako linie Kα2, je známa separace dubletu δ, je znám poměr intenzit linií R21=0.5. Tradiční metodou je Rachingerova korekce, která spočívá v prostém postupném odečítání intenzit profilu dubletu ze strany nižších úhlů |
| 3. Korekce na různé úhlově závislé faktory | Jedná se o faktory specifické pro užité záření a difrakční geometrii |
| 4. Vyhlazování profilů | V případě menšího počtu pulsů bývají difrakční data zašuměná a je třeba je vyhlazovat. To lze provést jednoduše lineárně či kubicky se zadaným vyhlazovacím okénkem. Velmi populární je např. metoda Savitzkého a Golaye, která je spojena s vyhledáváním píků pomocí derivací. Při vyhlazování je ovšem třeba dát pozor na možnou deformaci píků |
| 5. Určení parametrů | Po provedených korekcích je možné určit parametr z definice (integrální intenzitu např. numerickou integrací) a jiné (poloha, šířka) vyplynou snadno z druhé derivace záznamu. |
V mnoha případech jsou jednotlivé difrakční profily více či méně překryté. Tato situace nastává pro silně defektní materiály nebo velmi jemné prášky, kdy jsou profily značně rozšířené. Dále se pravděpodobnost překryvu zvyšuje u látek s nižší symetrií či velkou elementární buňkou, které mají větší počet difrakcí v měřeném oboru. Značné problémy činí i difraktogramy směsí více látek. Speciálním případem jsou tenké vrstvy, jejichž většinou značně široké difrakční linie se překrývají s píky od substrátu. Někdy nelze v záznamu ani změřit dobře pozadí. Za této situace je východiskem aproximace difrakčních profilů vhodnými analytickými funkcemi a pomocí nelineární metody nejmenších čtverců tak nalézt parametry těchto funkcí.
V praxi se používá několik funkcí. Jako základní jsou známé dvě - Gaussova a Lorentzova (nazývaná též Cauchyova). První se vyznačuje širším zvonovitým píkem a rychle spadajícími chvosty, zatímco druhá ostřejším píkem a dlouhými chvosty. Ve většině případů však pro rtg difrakci nepostačují, protože jim právě chybí tvarový faktor. Proto se používají obecnější funkce a to především Pearsonova (VII), která je v podstatě Cauchyho funkcí s obecným exponentem. Pravděpodobně nejoprávněnější je funkce Voigtova - konvoluce Gaussovy a Cauchyho funkce. Kvůli větší výpočetní náročnosti je však často dávána přednost tzv. pseudo-Voigtově funkci, což je prostý součet Gaussovy a Cauchyho funkce s volným parametrem vážícím obě složky. Někdy se též používá racionální lomená funkce.
Aproximace analytickými funkcemi ("fitování") |
Ve funkcích jsou jako Ai
vyznačeny rafinovatelné parametry: |
| Gaussova |
|
| Cauchyova |
|
| Pearsonova |
|
| Voigtova |
|
| Pseudo-Voigtova |
|
| Racionální |
|
Uvedené funkce se použijí pro obě složky dubletu a fituje se součet všech funkcí popisujících jednotlivé píky v měřeném segmentu difraktogramu.
Maximum difrakční linie lze určit několika způsoby:
Derivační metody je obvykle nutné spojit s vyhlazováním.
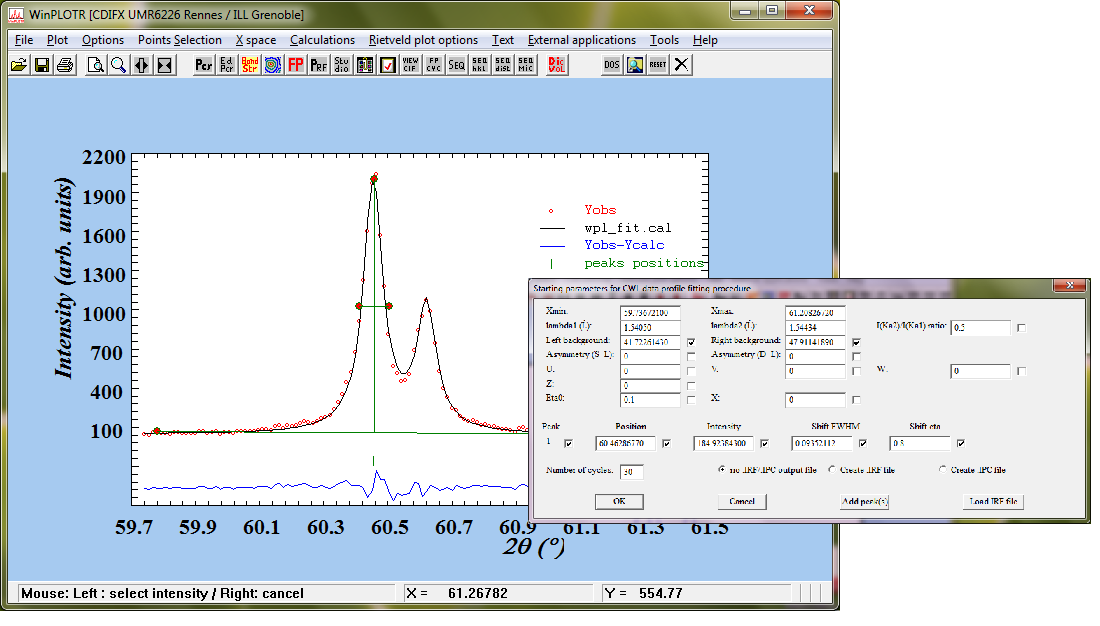
V dnešní době existuje řada programů pro vyhodnocování práškových difraktogramů. Několik jednodušších je k dispozici zdarma. Komerční systémy nabízející komfort a řadu možností jsou velmi drahé (desítky tisíc korun). V naší laboratoři je k dispozici místní program Difpatan pro DOS (obrazovka), kvalitní český komerční program ZDS (obrazovka) a v úloze na praktiku se nejčastěji používá volně dostupný krystalografický program WinPlotr.
|
|
Vyhodnocení difrakčního záznamu v programu WinPlotr. |