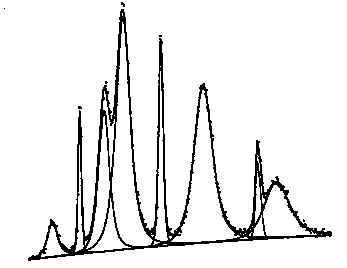

Praskovy rentgenovy difraktogram obsahuje radu cenny udaju o mikrostrukture zkoumaneho materialu. Jelikoz je ovsem rentgenova difrakce, na rozdil napr. od elektronove mikroskopie, metodou neprimou, neni vzdy jednoduche vsechny obsazene informace desifrovat. Prvnim nezbytnym krokem je co mozno nejpresnejsi urceni parametru namerenych difrakcnich profilu jednotlivych difrakci a dale korekce instrumentalnich vlivu.
Profil rtg difrakcni linie lze vyjadrit jako zavislost merene difraktovane intenzity I, nejlepe v pulsech za jednotku casu, na difrakcnim uhlu Q resp. 2Q. Nekdy je vhodne pouzivat stupnici reciprokych mezirovinnych vzdalenosti (difrakcniho vektoru) s = 2 sin Q/l.
Profil je mozne charakterizovat nekolika parametry, ktere primo souvisi s nekterymi strukturnimi a mikrostrukturnimi charakteristikami materialu, jak je uvedeno v nasledujicim schematickem prehledu.
Polohy difrakcnich piku (Qo) |
mrizove parametry - geometrie krystalove mrize - poruchy krystalove mrize, zbytkova napeti |
| kvalitativni fazova analyza | |
Integralni intenzity (I) |
struktura krystalove mrize (strukturni motiv, druh atomu, ..) |
| ~ ozareny objem vhodne orientovanych krystalitu - prednostni orientace krystalitu, kvantitativni fazova analyza | |
| Debyeovy-Wallerovy faktory (stredni kvadraticke vychylky atomu) | |
Sirky |
velikost koherentne difraktujicich oblasti - krystalitu |
| vnitrni nehomogenni mikroskopicka napeti, poruchy krystalove mrize (dislokace, dislokacni smycky) | |
Tvarove parametry |
rozdeleni poruch, velikosti castic, indikace typu poruch |
Polohy a intenzity lze pri neprilis vysokych narocich na presnost urcovat i ze spojitych zaznamu. Pro studium sirek a tvaru profilu je vsak treba provest podrobnejsi analyzu a pro efektivni zpracovani je samozrejme nutne uzit krokovy zaznam a digitalni zpracovani.
V soucasnosti existuji asi tri skupiny metod zpracovani difrakcnich zaznamu:
Prima analyza |
predpoklada moznost spravneho urceni pozadi, ktere je meritelne na obou stranach profilu |
| 1. Separace pozadi | je komplikovanejsi pri znacne rozsirenych profilech, kdy je tendence pozadi precenit. I kdyz ne vsechny prispevky k pozadi jsou linearni s difrakcnim uhlem, casto se aproximuje pozadi primkou. Za oblst, ve ktere se meri, lze vzit takovou, kde ho je mozne na obou stranach piku aproximovat stejnou linearni zavislosti. |
| 2. Korekce na dublet | Pri pouziti klasickych zdroju zareni a
beznych praskovych difraktometru pracujeme vzdy s dubletem Ka1,a2. Pro presnou analyzu profilu a zvlaste pro jeji spravnou interpretaci je treba provest separaci linie Ka2. Byla publikovana rada postupu, z nichz vetsina je zalozena na trech predpokladech: profil slozky Ka1 ma stejny tvar jako linie Ka2, je znama separace dubletu d, je znam pomer intenzit linii R21=0.5. Tradicni metodou je Rachingerova korekce, ktera spociva v prostem postupnem odecitani intenzit profilu dubletu ze strany nizsich uhlu |
| 3. Korekce na ruzne uhlove zavisle faktory | Jedna se o faktory specificke pro uzite zareni a difrakcni geometrii |
| 4. Vyhlazovani profilu | V pripade mensiho poctu pulsu byvaji difrakcni data zasumena a je treba je vyhlazovat. To lze provest jednoduse linearne ci kubicky se zadanym vyhlazovacim okenkem. Velmi popularni je napr. metoda Savitzkeho a Golaye, ktera je spojena s vyhledavanim piku pomoci derivaci. Pri vyhlazovani je ovsem treba dat pozor na moznou deformaci piku |
| 5. Urceni parametru | Po provedenych korekcich je mozne urcit parametr z definice (integralni intenzitu napr. numerickou integraci) a jine (poloha, sirka) vyplynou snadno z druhe derivace zaznamu. |
V mnoha pripadech jsou jednotlive difrakcni profily vice ci mene prekryte. Tato situace nastava pro silne defektni materialy nebo velmi jemne prasky, kdy jsou profily znacne rozsirene. Dale se pravdepodobnost prekryvu zvysuje u latek s nizsi symetrii ci velkou elementarni bunkou, ktere maji vetsi pocet difrakci v merenem oboru. Znacne problemy cini i difraktogramy smesi vice latek. Specialnim pripadem jsou tenke vrstvy, jejichz vetsinou znacne siroke difrakcni linie se prekryvaji s piky od substratu. Nekdy nelze v zaznamu ani zmerit dobre pozadi. Za teto situace je vychodiskem aproximace difrakcnich profilu vhodnymi analytickymi funkcemi a pomoci nelinearni metody nejmensich ctvercu tak nalezt parametry techto funkci.
V praxi se pouziva nekolik funkci. Jako zakladni jsou zname dve - Gaussova a Lorentzova (nazyvana tez Cauchyova). Prvni se vyznacuje sirsim zvonovitym pikem a rychle spadajicimi chvosty, zatimco druha ostrejsim pikem a dlouhymi chvosty. Ve vetsine pripadu vsak pro rtg difrakci nepostacuji, protoze jim prave chybi tvarovy faktor. Proto se pouzivaji obecnejsi funkce a to predevsim Pearsonova (VII), ktera je v podstate Cauchyho funkci s obecnym exponentem. Pravdepodobne nejopravnenejsi je funkce Voigtova - konvoluce Gaussovy a Cauchyho funkce. Kvuli vetsi vypocetni narocnosti je vsak casto davana prednost tzv. pseudo-Voigtove funkci, coz je prosty soucet Gaussovy a Cauchyho funkce s volnym parametrem vazicim obe slozky. Nekdy se tez pouziva racionalni lomena funkce.
Aproximace analytickymi funkcemi ("fitovani") |
Ve funkcich jsou jako Ai
vyznaceny rafinovatelne parametry: |
| Gaussova |
|
| Cauchyova |
|
| Pearsonova |
|
| Voigtova |
|
| Pseudo-Voigtova |
|
| Racionalni |
|
Uvedene funkce se pouziji pro obe slozky dubletu a fituje se soucet vsech funkci popisujicich jednotlive piky v merenem segmentu difraktogramu.
Maximum difrakcni linie lze urcit nekolika zpusoby:
Derivacni metody je obvykle nutne spojit s vyhlazovanim.
V dnesni dobe existuje rada programu pro vyhodnocovani praskovych difraktogramu. Nekolik jednodussich je k dispozici zdarma. Komercni systemy nabizejici komfort a radu moznosti jsou velmi drahe (desitky tisic korun). V nasi laboratori je k dispozici mistni program Difpatan pro DOS (obrazovka) a kvalitni cesky komercni program ZDS (obrazovka)