The crystal structure of aromatic molecules under high pressure

M. Oehzelt¹, G. Heimel¹, A. Aichholzer¹, P. Puschnig², K. Hummer², C. Ambrosch-Draxl², M. Hanfland³, F. Porsch⁴, A. Nakayama⁵, R. Resel¹

¹Institute of Solid State Physics, Graz University of Technology, Petersgasse 16, A-8010 Graz, Austria.

²Department for Physics - Theoretical Physics, University of Graz, Universitätsplatz 5, A-8010 Graz, Austria.

³European Synchrotron Radiation Facility, BP 220, F-38043 Grenoble, France.

⁴Institute of Mineralogy and Petrology, University of Bonn, Poppelsdorfer Schloß, D-53115 Bonn, Germany.

⁵Reserach Center for Advanced Carbon Materials, National Institute of Advanced Industrial Science and Technology, Tsukuba, Ibaraki 305-8565, Japan.

In the last three decades, π-conjugated hydrocarbon materials have attracted a lot of attention. In particular, organic polymers seem to be promising candidates for low-cost, easy-processing materials for electro-optical and electronic applications. Significant insight into many properties of these materials can often be gained by studying a single, isolated molecule (e.g. in solution). Nevertheless, for transport phenomena determining the performance of (opto)electronic devices, intermolecular interaction in terms of wavefunction overlap and low frequency (external) phonons will play a crucial role. Moreover, important optical features such as the luminescence quantum yield in the solid state can drastically differ form that of single molecules. Last but not least, the strong anisotropy of the conductivity and the dielectric function often found in crystals of short polycyclic organic molecules is closely related to the specific way of molecular packing. Hence, a detailed understanding of the crystal structure and the arrangement of the molecules relative to each other is a prerequisite for understanding important bulk and thin film properties in this classes of materials.

A deeper insight into the nature of the intermolecular interactions and the packing forces acting between the molecules can be gained by modulating the intermolecular distances. Applying pressure to the sample is a ‘clean’ way to tune the degree of intermoleculear interaction. There are essentially two different kinds of atom-atom interaction in molecular crystals. On one hand there are strong, covalent intramolecular bonds and, on the other hand, there are weak, van der Waals-type forces acting between separate molecules. This fact justifies to regard the molecules as rigid. Applying pressure brings the whole molecular units closer together and/or changes their arrangement relative to each other.

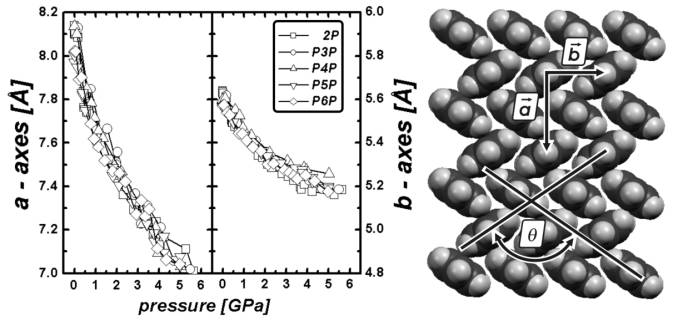
Figure 1: Lattice parameter a (left panel) and b (right panel) of the oligo(para)-phenylenes containing two to six phenyl rings as a function of hydrostatic pressure. The lattice parameters of all oligomers have the same length at ambient conditions and show the same pressure dependence. The left and right y axis cover the same range (1.2 Å). Note that the lattice constant a is reduced approximately twice as much as the lattice constant b in this pressure region. The pictogram on the right side shows a projection of the crystal structure of the oligo(para)-phenylenes vizualizing the two lattice parameters a, b and the herring bone angle q.

This work is a summary of measurements performed over several years. The samples for all measurements were crystalline powders. The considered materials are the oligo-acenes (anthracene - C₁₄H₁₀, tetracene - C₁₈H₁₂, pentacene - C₂₂H₁₄), the oligo-phenylens (from biphenyl - C₁₂H₁₀ to hexaphenyl - C₃₆H₂₆), fluorene - C₁₃H₁₀, and perylene - C₂₀H₁₂. Anthracene was measured at the photon factory BL18C (Tsukuba, Japan)[1,2], the whole series of oligo-acenes and oligo-phenylenes at Hasylab BL F3 (Hamburg, Germany)[3,4], fluorene and perylene at ESRF ID 9 (Grenoble, France) [work in progress]. All experiments, except at the Hasylab BL F3 which is an energy dispersive x-ray diffraction (EDXD) beam line, are done on angle dispersive x-ray diffraction (ADXD) beam lines. The advantage of ADXD over EDXD is the amount of information that can be drawn from the diffraction data. In case of ADXD, the diffraction data could be refined with the Rietveld method and in addition to the change of the lattice constants, the rearrangement of the molecules (considered as rigid bodies) within the unit cell could be determined. Pressures up to 22 GPa were applied using diamond anvil cells (DAC).

In case of these soft organic materials it is of major importance to guarantee appropriate hydrostatic conditions. For example anthracene undergoes a phase transition if it is not isotropically compressed [5], but it does not show a crystallographic phase transition up to at least 22 GPa under hydrostatic conditions. In the case of fluorene we observe a phase transition at 3.5 GPa under hydrostatic conditions [paper in preparation]. The structure remains in the orthorhombic space group but the angle of the herringbone pattern q (see figures 1, 2) decreases significantly and an almost p-stacked regime is formed. The herringbone angle changes from around 120° to around 60° during the transition, while any compression in a non-hydrostatic environment results in a phase transition at even lower pressures.

Figure 1 shows the summary of changes in the ab-plane of the oligo-penylenes obtained by EDXD measurements. Note that the lattice constant a changes twice as much as the lattice constant b. This behaviour results in an effective rotation of the molecules to higher herringbone angles q which is similar for all oligo-phenylenes. The same behaviour of a changing twice as much as b is shown in the oligoacenes. ADXD measurements of anthracene reveal more details in the changing of the molecular packing. The rearrangement of the molecules under pressure has a high impact on the band structure as well as on the optical properties [4,6]. For example a redshift and a broadening of the optical transition under pressure is observed, which has a purely intermolecular origin.

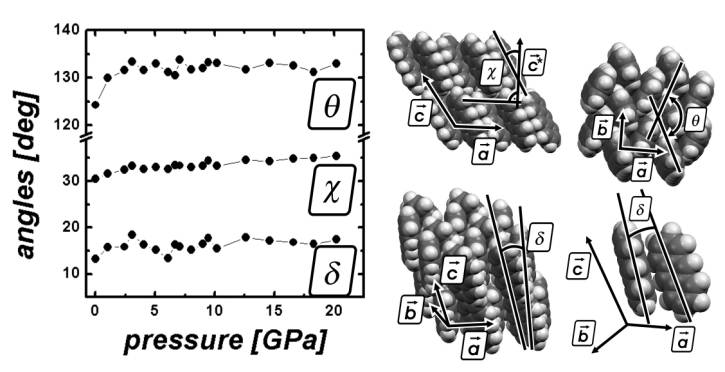
Figure 2: Rearrangement of the anthracene molecules under pressure visualized by the angles q, c, and d. q is the herringbone angle and defined as the angle between the molecular planes of the two translationally inequivalent molecules. The setting angle between the long molecular axis and the c* axis is denoted by c, whereas the tilt angle between the two long molecular axes of translational inequivalent molecules is given by d.

Acknowledgement

This research project is supported by the Austrian Science Fund (Project No. P15626-PHY). M.O. also likes to acknowledge the Austrian Research Society (ÖFG).

[1] M. Oehzelt, R. Resel, A. Nakayama, Phys. Rev. B 66 (2002) 174104.

[2] M. Oehzelt, G. Heimel, R. Resel, P. Puschnig, K. Hummer, C. Ambrosch-Draxl, K. Takemura, A. Nakayama, J. Chem. Phys. 119 (2003) 1078.

[3] G. Heimel, P. Puschnig, M. Oehzelt, K. Hummer, B. Koppelhuber-Bitschnau, F. Porsch, C. Ambrosch-Draxl, R. Resel, J. Phys.: Condens. Matter 15 (2003) 3375.

[4] P. Puschnig, K. Hummer, C. Ambrosch-Draxl, G. Heimel, M. Oehzelt, R. Resel, Phys. Rev. B 67 (2003) 235321.

[5] R. Resel, M. Oehzelt, K. Shimizu, A. Nakayama, K. Takemura, Solid State Comm. 129 (2004) 103.

[6] K. Hummer, P. Puschnig, C. Ambrosch-Draxl, Phys. Rev. B 67 (2003) 184105; Phys. Rev. Lett. 92 (2004) 147402.