Powder Diffraction Study of Thermal Expansion and Crystal Structure of the Aurivillius Phases in the Bi4Ti3O12

Powder Diffraction Study of Thermal Expansion and Crystal Structure of the Aurivillius Phases in the Bi₄Ti₃O₁₂–BiFeO₃ System

M. Krzhizhanovskaya¹, S. Filatov¹, V. Gusarov², P. Paufler³, E. Antoshchenkova¹, R. Bubnova², M. Morozov², D. Meyer³

¹Dept. of Crystallography, St. Petersburg State University, University Emb. 7/9, St. Petersburg 199034, Russia

²Institute of the Silicate Chemistry of Russ. Acad. of Sci., Ul. Odoevskogo, 24/2, St. Petersburg 199155, Russia

³Institut für Strukturphysik, Technische Universität Dresden, D-01062, Dresden, Germany

The Aurivillius family of layered Bi-containing oxides is well known for its ferroelectric properties. Usually their crystal structure is described as a combination or intergrowth of (Bi₂O₂)²⁺ layers and (A_n-1B_nO_3n+3)^2- perovskite–like blocks, where A is a twelve co-ordinated cation e.g. Na, K, Ca, Sr, Ba, Pb, Bi, etc. and B is an octahedral cation such as Fe, Ti, Nb, Ta, Cr, etc.

In the Bi₄Ti₃O₁₂ – BiFeO₃ system the compounds with general chemical formula Bi₂Bi_n-1(Ti,Fe)_nO_3n+3, n = 3, 3.5, 4, 4.5, 5, 6, 8 synthesised by solid state reaction are noted in [1]. The crystal structures of the compounds with n = 3, 3.5, 4 are determined in orthorhombic system in [2], [3], [4] respectively. The structure of Bi₄Ti₃O₁₂ (n=3) is refined by Rietveld method in orthorhombic space group B2cb at 25, 500 and 650 ^oC and in tetragonal space group I4/mmm at 800 ^oC [5]. For Bi₅Ti₃FeO₁₅ (n=4) the polymorph phase transition from polar orthorhombic A2₁am space group to tetragonal I4/mmm is studied in details by Rietveld method using PND data [6]. 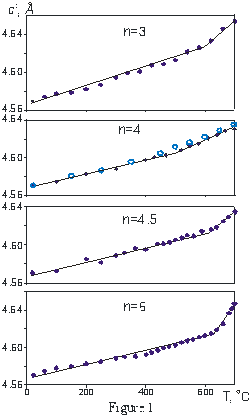Its transition temperature determined as ~ 730 ^oC is coincident with Curie temperature corresponded to ferroelectric-paraelectric transition.

Now we investigate the thermal behaviour of four aurivillius phases with n = 3, 4, 4.5 and 6 using high-temperature X-ray powder diffraction in air (CuKa-radiation, the temperature range 20-700 ^oC) and DTA method (20-1300 ^oC). The temperature dependence of c cell parameter counting on a perovskite layer (c’) is presented in Fig. 1 along with the data from [6] for n=4. The dependence is obviously divided into two ranges: the low temperature region with a lower thermal expansion and a high temperature region with a greater expansion. The linear thermal expansion coefficient a_c for HT phase is 3 times larger than that one for LT phase. Since a and b cell parameters (5.46+0.03 Å) and correspondingly the paired hkl, khl reflections are very close to each other in the studied compounds, it is complicated to calculate a and b values correctly. To define the orthorhombic-tetragonal transition point we analyze the FWHM temperature changes for unique and paired reflections. For example for Bi₅(Ti,Fe)₄O₁₅ (n=4) the FWHM of the reflection hkl : 119 (I/Io=100%) practically does not change under heating: 0.33 ^o2q at 20 ^oC and 0.31at 640 ^oC. FWHM of paired reflection 200 and 020 (I/Io=30%) decreases from 0.45 ^o2q at room temperature up to 0.31 at 640 ^oC. If the orthorhombic structure transfers to tetragonal the FWHM of unique and paired reflections becomes equal. Also a weak endothermic effect is observed on the DTA curve in the range of temperatures 650-740 ^oC in all studied samples. The Table 1 contains the following specific temperature points: (1) the inflection point of c cell parameter vs. temperature; (2) the temperature point in which the FWHM of unique and paired reflections becomes equal; (3) the DTA endothermic effect. Clearly, that the temperature of DTA effect is always higher than the changes in XRD pattern on heating. It could be caused by a different heating rate.

Table 1. Thermal behaviour of aurivillius phases from HTXRD and DTA data. Specific temperature points (^oC): (A) the inflection point of c cell parameter vs. temperature; (B) FWHM of paired peaks is equal to that of unique; (C) DTA endothermic effect

	A	B	C
n=3	610	660	660
n=4	500	640	740
n=4.5	600	600	690
n=6	620	620	650

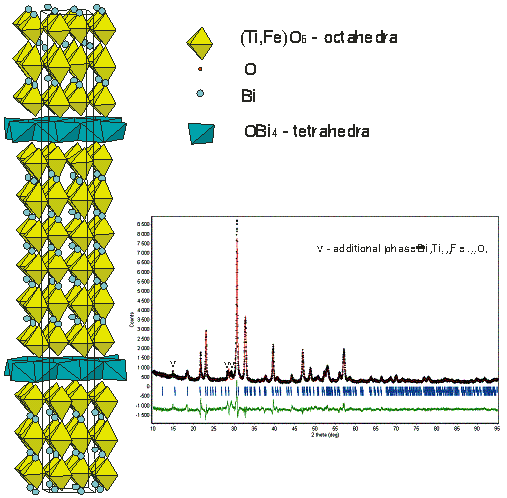
As far as we are aware, there is only one crystal structural study of Aurivillius phase structure with c parameter 57.6 Å corresponded to a 6 layer-structure [7]. For Bi₇Ti₃Fe₃O₂₁ we propose the structural model based on 6 layered perovskite blocks. To build up the model the atomic coordinates of Bi₅Ti₃FeO₁₅ [4] were used. It was refined in orthorhombic Fmm2 space group: a=5.474(1), b=5.495(1), c=57.60(1) Å with Rietica for Rietveld refinement program (Rp = 10.2, Rwp = 13.3, R_B=5.6%). It was also refined in A2₁am space group but no additional reflections which are compatible with this lower symmetry were observed. Relatively high R-factors are caused probably by the structure defects. The FWHN for reflection of 00l type is two-three times larger than that one for other reflections. Perhaps the number of layers in block is not constant in the structure, but the considerable amount of 6-layer phase is present. This structure could also be described in terms of crystal chemistry with oxocentered anions as an alternation of perovskite blocks and Bi-O layers build up from OBi₄ tetrahedra by sharing edges (Figure 2).

Figure 2. The Crystal structure of Bi₇Ti₃Fe₃O₂₁and the Rietveld data plot.

1. M.I. Morosov, V.V. Gusarov, Inorg. Materials 38 (2002) 723-729

2. G.N. Subbanna, T.N. Guru Row, C.N.R. Rao, J. Solid State Chem. 86 (1990) 206-211

3. B. Aurrivillius Ark. Kemi. 1 (1949) 463-471, 499-512, 519-528

4. C.H. Hervoches et al. J. Solid State Chem. 164 (2002) 283-286

5. C.H. Hervoches and P. Lightfoot, Chem. Mater. 11 (1999) 3359-3364

6. A. Snedden, C.H. Hervoches, P.Lightfoot Phys. Review B67 (2003)

7. D. Mercurio, G. Trolliard, T. Hansenand, J. P. Mercurio, Int. J. Inorg. Mater. 2 (2000) 397-406