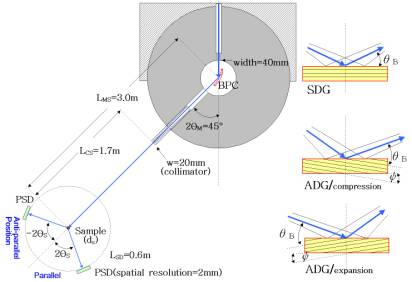
Bent perfect crystal (BPC) monochromator at the monochromatic focusing conditions

Bent perfect crystal (BPC) monochromator at the monochromatic focusing condition

Y. N. Choi¹, S.A. Kim¹, S.K. Kim¹, S.B. Kim¹, C.H. Lee¹, P. Mikula², M. Vrána²

¹HANARO Centre, Korea Atomic Energy Research Institute, Yuseong, Daejeon 305-600, Korea

²Nuclear Physics Institute and Research Centre Řež, Ltd., 25068 Řež near Prague, Czech Republic.

Conventional neutron diffractometers employing a single mosaic monochromators are oerated only in the parallel (+,-) measurement setting, because the resolution property of the anti-parallel (+,+) setting is much worse [1]. However, if we could use the both setting with the equivalent resolution, the measurement efficiency could be twice of that related to the traditional measurement mode. A strong difference in the resolution properties in the parallel and antiparallel settings is brought about by a nonnegligible l-q correlation of the monochromatized beam impinging the sample in the scattering plane. In order to overcome this problem the momentum distribution of the monochromatized neutrons should be symmetric with respect to the axis of the beam impinging the sample. Three monochromator arrangements which could provide a rather highly collimated monochromatic neutron beam with a negligible l-q correlation with a reasonable Dl (keeping the luminosity and the instrument resolution on an acceptable level) have been already tested, namely:

1. Fully asymmetric diffraction (FAD) geometry of the Si-BPC monochromator [2-4]. The FAD geometry of the monochromator is in fact a limiting case of the Fankuchen geometry which implicates some limitations on a choice of the crystal. At present, a bent perfect Si-crystal with a very low attenuation for neutrons could be the best candidate for this purpose. According to our information, the FAD geometry of the monochromator has not been employed for a routine work, though some tests of the FAD monochromator systems have been already carried out [2-4].

2. Dispersive double-crystal setting [5-8]. A strongly dispersive double-crystal arrangement of two mosaic or bent perfect crystals or combination of them is another monochromator performance having a negligible q-l correlation of the monochromatic neutrons in the scattering plane but providing a sufficient neutron current at the sample position represents. The strongly dispersive double crystal setting can be achieved either by using two crystals with the same lattice constant mutually in the antiparallel (+,+) arrangement or by using two crystals with a large difference in the lattice constants.

Fig. 1. Experimental set-up at ST1 beam port of the HANARO reactor and three diffraction geometries used in the test.

3. Multiple reflection Umweganregung monochromator [7-10]. Umweganregung monochromator is based on a multiple Bragg diffraction process (often referred to as simultaneous reflections) realised in one crystal and can be observed when a crystal lattice is oriented in such a way that more than one set of planes are simultaneously operative for a given wavelength. In the extreme case the Umweganregung effect going through a secondary and tertiary reflection can simulate forbidden primary reflection [11-13]. It has been already demonstrated [7, 9,10] that strong multiple reflection effects resulting in Umweganregung and observed in elastically deformed perfect crystals can be used for ultra-high monochromatization and diffraction studies.

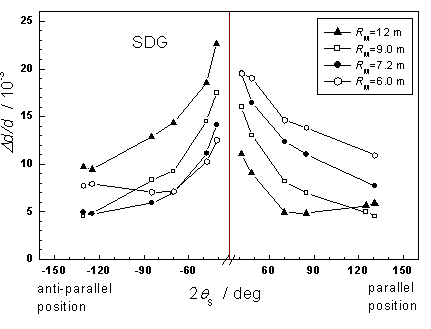
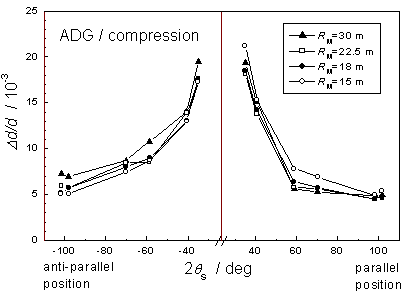
This contribution deals with another performance of the BPC monochromator adjusted for the monochromatic focusing. Contrary the above mentioned monochromator performances where a narrow (negligible q-distribution) phase-space element with a reasonable Dl is aligned parallely to the beam axis, in this case a narrow phase-space element with quite a large q-distribution but small l-distribution is aligned perpendicularly to the beam axis. As will be shown, the BPC monochromator at monochromatic focusing condition can provide equal resolution property at both (+,-) as well as (+,+) settings and gives a chance to use both sides of the scattering half-plane. Three diffraction geometries (symmetric, asymmetric with the diffracted beam compression and asymmetric with the diffracted beam expansion) with BPC monochromators were tested. As schematically shown in Fig. 1, three typical diffraction geometries were chosen to investigate the dependence of the FWHM of the line profiles and the resolution the corresponding (Dd/d)-resolution (the (Dd/d)- data were calculated from the FWHM-data) on the monochromator bending radius. For the SDG-experiment, a Si(220) crystal slab of the dimensions of 200x30x3 mm³ was used. For the ADG/compression and ADG/expansion experiments, Si(211) crystal slab (thickness of 3.8 mm) with 311 planes at Y=10^o and a special cut of silicon slab (thickness of 3.8 mm) with the planes (311) at Y=20°, respectively, were used. The calculated values of the bending radii R_MF corresponding to individual geometries are 7.84 m, 13.9 m and 4.46 m, respectively. Figs. 2-4 display the experimental results obtained with three different monochromator crystals and demonstrate that when R approaches to R_MF, the resolution property becomes equivalent in both diffraction geometries.

Fig. 2. Experimental data of Dd/d resolution for Si(220) (l = 0.147 nm) crystal slab set in symmetric diffraction geometry (q_M=22.5^o, R_MF= 7.84 m).

Fig. 3. Experimental data of Dd/d resolution for Si(311) (l=0.125 nm) crystal slab set in asymmetric diffraction geometry with the out beam compression (q_M-Y =12.5^o, R_MF= 13.9 m).

Fig. 4. Experimental data of Dd/d resolution for Si(311) (l=0.125 nm) crystal slab set in asymmetric diffraction geometry with the out beam expansion (q_M +Y =42.5^o, R_MF= 4.46 m).

In principle, the measurement efficiency in powder diffractometry could be increased twice and the range of scattering angles could be substantially extended. In the case of the strain measurements the monochromatic focusing performance permits a measurement of two strain components simultaneously. Another application of such focusing monochromator could be for inelastic scattering experiments on triple axis spectrometer. (DE/E)-resolution is then determined by the lateral dimension of the sample and the effective mosaicity of the BPC monochromator which is about one order of magnitude smaller that the mosaicity of conventional mosaic monochromators. Of course, similarly to the BPC-monochromator, a BPC-analyser at the monochromatic focusing condition could also be used, though due to a generally smaller sample-analyser distance L_SA (L_SA<L_MS) the bending radius of the analyser R_MF is correspondingly smaller.

Acknowledgement

We are grateful to the in-house collaborators, Mr. B.H. Choi, Mr. Y.H. Choi, Mr. K.P. Hong, Dr. M.K. Moon and Dr. V.T. Em for the experimental preparations and to Ms. H.S. Oh for the numerous data processing. This work was in Korea supported by the Korean Ministry of Science and Technology through the National Nuclear R&D Programme and the Scientist Visiting Program and in the Czech Republic by the research projects GA-CR (No. 202/03/0891), GA-CAS (No. A1048003) and COST – OC P7.003 and MSM2672244501.

1. G. E. Bacon, Neutron Diffraction, Clarendon Press, Oxford (1975) pp.101-111.

2. P. Mikula, P. Lukáš and R. Michalec, J. Appl. Cryst. 20 (1987) 428-430.

3. P. Mikula, J. Kulda, L. Horalík, B. Chalupa and P. Lukáš, J. Appl. Cryst. 91 (1986) 324-330.

4. M.R. Muslih, I. Tanaka, P. Mikula, N. Niimura, JAERI Review 2002-028, p. 119.

5. P. Mikula et al., Mater. Sc. Forum, Vols. 404-407 (2002) 299-302.

6. M. Popovici and A.D. Stoica, Appl. Phys. A 74 (2002), S273-S276.

7. P. Mikula, M. Vrána, V. Wagner, Y. N. Choi, S. A. Kim, H. S. Oh, K. H. Sung and C. H. Lee, Proc. of Int. Conf. ATEM´03, Sept. 10-12, 2003, Nagoya, Japan. CD ROM Published by JSME No. 03-207, paper OS04W0288.

8. M. Vrána, P. Mikula, R.T. Michalec, J. Kulda and J. Vávra , Acta Cryst. A 37 (1981) 459-465.

9. P. Mikula, J. Kulda, M. Vrána, R.T. Michalec and J. Vávra, Nucl. Instrum. Methods, 197 (1982) 563-566.

10. P. Mikula et al., Proc. of the Symp. Neutron Scattering, August 6-8, 1984, West Berlin, HMI-B 411, p. 233-235.

11. M. Renninger, Z. Phys. 106 (1937) 141-176.

12. R.M. Moon and C.G. Shull, Acta Cryst. 17 (1964) 805-812.

13. Shih-Lin Chang, Multiple Diffraction of X-rays in Crystals, Springer Verlag, 1984; Moscow "Mir", 1987.