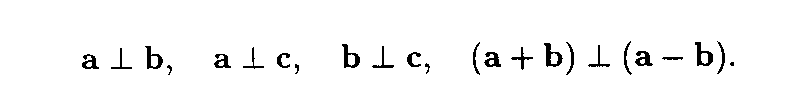
ON THE 'DISTANCE' OF A LATTICE FROM A GIVEN BRAVAIS TYPE

Boris Gruber

Faculty of Mathematics and Physics, Charles University, Malostranske n'am.25, 118 00 Praha 1, Czech Republic

Keywords: Lattice, Bravais type, distance

A quantitative measure for determining `how much' a lattice differs from a given Bravais type is proposed. It has a clear crystallographic meaning and is suitable for computer calculation.

To determine the Bravais type of a lattice requires to decide between equalities and inequalities of certain lattice parameters. This may be done - strictly speaking - only when the values of these parameters are known exactly. If, however, the lattice parameters are ascertained by measurement the above decision is in principle impossible. Here instead of trying to attach a unique Bravais type to a given lattice as its Bravais type it seems more frank to ask `how far' this lattice is from an (in principle arbitrary) Bravais type in which we are at that moment interested. The goal of this contribution is to suggest a sensible definition of this `distance'.

Our method is based on the observation that the shape of conventional cells of lattices of a given crystal family can be fully characterized by mere right angles. For example, the tetragonal conventional cells by

 

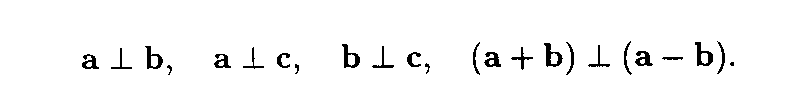
The deviations from these right angles may serve as a natural means for the construction of the concept we are seeking. Thus our `distance' will be a dimensionless number meaning an angle. We shall introduce it gradually in three successive steps.

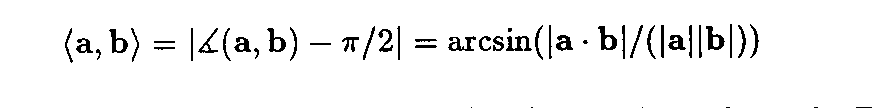
  1. If a, b are non-zero vectors we define

and call this number the distance of the angle < (a, b) from the right angle. For example, in this notation the conventional cells of monoclinic lattices can be characterized by the requirement that the number

Max (<a, b>, <b, c>)

is equal to zero.

  1. If Q = (a, b, c) is a cell (primitive or centered) we define
    d(Q,m) = Min[Max(< a, b >, < b, c >), Max( < b, c >, < c, a >), Max (< c, a >, < a, b > )]
    (= the number between the smallest and the greatest}and call this number the distance of the cell Q from the crystal family ~ m. In a similar but often more complicated way the distance d(Q,x) of Q from an arbitrary crystal family x is introduced.
  2. Let L be a lattice and xY an arbitrary Bravais type, let Y(L) denote the set of all cells of L with the centering Y. Then we define

  4. and call this number the distance of the lattice L from the Bravais type xY.

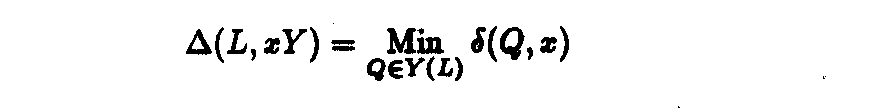
An algorithm for determining the number (1) is not known to us and a direct calculation is not possible since the set Y(L) is infinite. A finite substitute is necessary. We shall realize it by taking in (1) only those cells Q of Y(L) whose edges are linear combinations with the coefficients 1, 0, -1 of the shortest vectors of sublattices of L defined by the centering Y[1]. Our conjecture is that in this way we get the number (1) exactly.

Whether this procedure can be practically used will appear when the computer program is completed.

1. B. Gruber, Cas. pest. mat. 95 (1970), 231-239