ATOMIC VOLUME AND CRYSTAL STRUCTURE OF ELEMENTS
S. Hübner, M. Trömel
Institut für Anorganische Chemie, Marie
Curie-Str. 11, 60439 Frankfurt, Germany
e-mail: sven@solid.anorg.chemie.uni-frankfurt.de
http://solid.anorg.chemie.uni-frankfurt.de/~sven/
Keywords: atomic volume, dense structures, bond order, atomic valence, high pressure modifications
1 Dense Structures
Modifications of elements with close-packed structures (fcc or
hcp) transform into each other almost without change of
volume ![]() [1]
and the same holds good for transformations fcc
[1]
and the same holds good for transformations fcc ![]() bcc and hcp
bcc and hcp ![]() bcc. Structures which
obey this rule are called 'dense'. VD
stands for their atomic volume. Density is defined as the number
of particles per volume unit.
bcc. Structures which
obey this rule are called 'dense'. VD
stands for their atomic volume. Density is defined as the number
of particles per volume unit.
Volume rule: Phase transitions between dense structures occur, in first approximation,without a change of atomic volume
Dense structures are fcc, hcp (with ![]() ), bcc and the
tetragonal body-centered structure with
), bcc and the
tetragonal body-centered structure with ![]() (Pa,
(Pa, ![]() -Mn, In, all of them
true metals) [2].
-Mn, In, all of them
true metals) [2].
2 Non-Dense Structures
From the definition of VD it follows
that ![]() , where VX
is the atomic volume in any structure X. So we can define the
volume factor fX:
, where VX
is the atomic volume in any structure X. So we can define the
volume factor fX:
| (1) |
Here a structure X is considered 'non-dense' if fX>1.01.
To calculate the volume factor fX for
any structure X we have to assume in addition to the validity of
the volume rule:
- The atomic valence W of an element is the same in the
dense and in the non-dense modifications
- Bond order s depends on the distance r of each neighbouring
atom according to
| (2) |
R1 and b are bond order parameters. The sum of the bond orders around each atom equals its atomic valence W:
| (3) |
fX then can be calculated by (see [1], [3]):
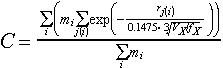 |
(4) |
| mi | = | multiplicity of the i-th atom |
| j(i) | = | geometrical coordination number [2] |
| rj(i) | = | distances from i to the j-th atom |
| C | = |
Using equation (1) the atomic volume of the dense modification can be determined from any structure X of an element. The example of phoshorus shows a rather good agreement between the atomic volume of the hypothetical dense modification of phosphorus calculated from different observed structures with largely differing atomic volumes:
| Pblack | 18.97 | 13.84 | 1.371 | [4] |
| PHittorf | 21.79 | 13.65 | 1.596 | [5] |
| P4 | 26.47 | 13.15 | 2.013 | [6] |
This result and some more [3] indicate the validity of equation (4) and the foregoing assumptions.
3 Atomic Volumes of High Pressure Modifications
The atomic volume of a dense modification VD
is expected to decrease smoothly with pressure. Fig. (1) shows
the calculated VD of phosphorus. VD
for normal pressure is extrapolated from this curve as
13.70(6) ![]() in
very good agreement with the average VD from Pblack
and PHittorf.
in
very good agreement with the average VD from Pblack
and PHittorf. 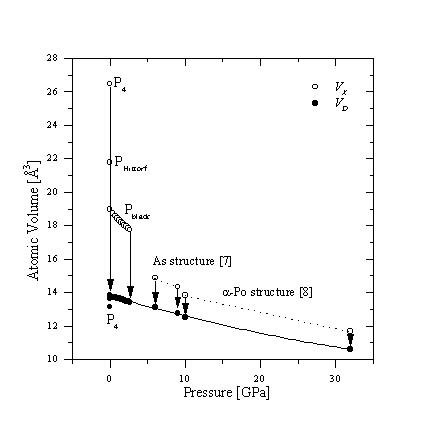 Figure 1: Observed atomic volumes VX
and calculated VD of phosphorus
depending on pressure
Figure 1: Observed atomic volumes VX
and calculated VD of phosphorus
depending on pressure
References
| [1] | Trömel, M., Hübner, S.: Z. Kristallogr. Suppl. 15 (1998) 92. |
| [2] | Alig, H., Trömel, M.: Z. Kristallogr. 201 (1992) 213-222. |
| [3] | Trömel, M., Hübner, S.: Z. Kristallogr. Suppl. 15 (1998) 85. |
| [4] | Cartz, L., Srinivasa S. R., Riedner R. J., Jorgensen J. D., Worlton T. G.: J. Chem. Phys. 71 (1979) 1718-1721. |
| [5] | Thurn H., Krebs, H.: Acta Cryst. B25 (1969) 125-135. |
| [6] | Simon A., Borrmann H., Craubner H.: Phosphorus and Sulfur and the Related Elements 30 (1987) 507-510. |
| [7] | Jamieson J. C.: Science 139 (1963) 1291-1292. |
| [8] | Kikegawa T., Iwasaki H.: Acta Cryst. B39 (1983) 158-164. |