DISPERSIVE ANOMALOUS DIFFRACTION STUDIES OF MODULATED STRUCTURES

V. Favre-Nicolin¹, S. Bos¹, E. Lorenzo¹, J.-L. Hodeau¹, W. Shepard², T. Neisius³

1Laboratoire de Cristallographie, CNRS BP166, 38042 GRENOBLE Cedex, FRANCE
2LURE, Bat. 209D, F-91045 ORSAY, FRANCE
3ESRF, F-38043 GRENOBLE Cedex, FRANCE
e-mail : favre@polycnrs-gre.fr

Keywords : anomalous diffraction, dispersive diffraction, MAD, synchrotron radiation, charge-density-wave, phase transitions.

X-ray experiments in the vicinity of resonant edge of an atom shows an energy dependence of the diffracted intensity, and the shape of intensity variations vs. the energy changes drastically with the phase of the structure factor. Biologists routinely use these variations to solve structures with MAD [1] (Multiple Anomalous Diffraction). This method can also be applied to solve complex inorganic structures, such as modulated ones.

Application to modulated structures : modulated structures (for example in Charge-Density-Wave (CDW) compounds) exhibit satellite reflections, which are a highly selective source of information about the CDW ground state. The measurement of both amplitude and phase for these satellite reflections thus provides an unique tool to determine the atomic displacements giving rise to the modulated structure and to retrieve the electronic instabilities at the origin of the CDW.

Dispersive diffraction : when we can measure only few reflections, it is important to obtain a good precision on the determination of the phase : this can be achieved if the whole I(E) spectrum around the absorption edge is measured. We have developped a dispersive diffraction setup [2] at the ESRF, which allows us to collect a whole I(E) spectra on a continuous range (200-800 eV) around an absorption edge, in a short oscillation scan [see fig. 1]. This enables us to measure from 10 up to 30 reflections in a few minutes, using a 2D detector, thus allowing easier study of phase transitions. For this new method, we have developped a software "DAD" to calibrate, normalize and correct the raw intensities before refinement.

fig. 1 : dispersive diffraction images on (TaSe4)2I : (a) above Tc, with two Bragg reflections. The line corresponds to the I(E) spectra, with high energies at the bottom of the image and low energies at the top. The minimum in intensity coresponds to the absorption edge. (b) below Tc, each Bragg reflection is surrounded by 8 satellite reflections (4 strong and 4 weak). Each line gives information about both amplitude and phase for the reflection.

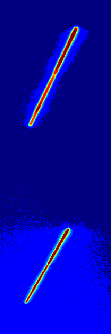(a) room temperature (b) T=100K

Sample studied : the transition metal tetrachalcogenide (TaSe₄)₂I is the focus of this study. This compound crystallises with tetragonal symmetry and consists of TaSe₄ chains which are parallel to the c-axis and separated by iodine atoms [3]. The metal-metal distances along the chain are found to be equivalent (3.2A) and their interaction is only through dz2 overlap. Given the number of electrons per metal site (0.5) and the symmetry considerations of the space group of the crystal (I422), the wavevector of the atomic modulation (2k_F) is at the centre of the Brillouin zone. X-ray studies have indicated 8 incommensurate reflections appearing below the phase transition temperature (TcA 265K) [4] at K=G+q where q=(±0.05, ±0.05, ±0.085), i.e., close to the Brillouin zone centre.

Further x-ray studies [5], based on measurements of the integrated intensities of 6 satellite reflections, have shown that the overall atomic displacements pattern is acoustic like, with a strong component of the displacements transverse to the chain axis. This result is at the odd of our understanding of CDW transitions, where one expects that antiphase metal atoms displacements along the chain direction be the most important and at the origin of the CDW state.

We will present results from experiments made on (TaSe₄)2I at the ESRF on ID24 beamline : we collected diffraction lines [see fig.1] both above and below Tc, for sublattice and satellite reflections. The recorded I(E) spectra will be compared with refinement taking into account (i) the acoustic model for the modulation from ref. [5] and (ii) shifts of Ta atoms along c, corresponding to the expected Ta tetramerization [6].

[1] W.A. Hendrickson , Science 254 (1991), 51,
[2] J-L. Hodeau et al., Rev. Sci. Inst. 66 (1995), (2)
[3] P. Gressier, L. Guemas and A. Meerschaut, Acta Cryst. B38 (1982), 2877
[4] H. Fujishita, M. Sato and S. Hoshino, Solid State Commun. 49 (1984), 313
[5] K.B. Lee, D. Davidov and A.J. Heeger, Solid State Commun. 54 (1985), 673
[6] J.E. Lorenzo, PhD. Thesis, University of Grenoble (1992) ; J.E. Lorenzo, R. Currat, P. Monceau, B. Hennion and F. Levy, Phys. Rev. B47 (1993), 10116