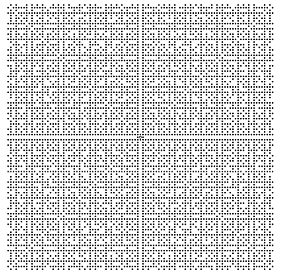Visible lattice points and weak model sets

Christian Huck

Fakultät für Mathematik, Universität Bielefeld (Germany),
huck@math.uni-bielefeld.de

Recently, the dynamical and spectral properties of square-free integers, visible lattice points and various generalisations have received increased attention; see [1,3] and references therein. One reason is the connection with Sarnak's conjecture on the `randomness' of the Möbius function, another the explicit computability of correlation functions as well as eigenfunctions for these systems. Here, we use the set V of points (x,y) of the square lattice Z² that are visible from the origin as a paradigm. Clearly, these are just the pairs with coprime corrdinates; see Fig. 1 for an illustration.

Figure 1. Central patch of V (left) and the diffraction of V restricted to the square [0,2]² (right).

By the Chinese Remainder Theorem, V has holes of arbitrary size and it is classic that the natural density exists and is equal to 6/π². It turns out that V has positive topological entropy equal to its density [4] and one thus might expect to leave the realm of pure point spectrum. However, V has pure point dynamical and diffraction spectrum [1,4]; see Fig. 1 and note that the disk areas represent the intensities. In fact, it is a major step to characterise the hull, i.e. the lattice translation orbit closure of V in the local topology. One can further show that the patch frequencies exist and this gives rise to a translation-invariant Borel probability measure on the hull. Our main result is that the corresponding measure theoretic dynamical system is isomorphic to a Kronecker system. Moreover, both the dynamical and the diffraction spectra are given by the points of Q² with square-free denominator. It turns out that all the examples mentioned above are weak model sets (the corresponding windows may have empty interior and a boundary of positive Haar measure) and it is thus natural to have a look at this abstract class of cut-and-project sets.

1. M. Baake & C. Huck, Proc. Steklov Inst. Math., 288, (2015), 165-188.

2. M. Baake, R. V. Moody, P. A. B. Pleasants, Discrete Math., 221, (2000), 3-42.

3. F. Cellarosi & Ya. G. Sinai, Europ. Math. Soc., 15, (2013), 1343-1374.

4. P. A. B. Pleasants & C. Huck, Discrete Comput. Geom.., 50, (2013), 39-68.

This work was supported by the German Research Foundation (DFG) within the CRC 701.