TWINS REVISITED: QUINARY TWINS AND BEYOND

Marianne QUIQUANDON, Abdullah SIRINDIL, Richard PORTIER, Denis GRATIAS

Paris-Sciences-Lettres, Institut de Recherche de Chimie Paris IRCP, 11 rue Pierre et Marie Curie, 75005 Paris, France

 

We define twin as being an external operation between two identical crystals that share a fraction of the atomic structure with no discontinuity from one crystal to the other. This includes merohedral twins, twin by reticular merohedry as well as coherent twin by contact  where only the habit plan is shared by the two adjacent crystals (epitaxy). Interesting and original cases appear when the invariant substructure is built with positions belonging to a same Z-module (irrational projection in d-dim space of a N-dim lattice, with N>d) as, for example, the quinary twin structure (C5-module) first drawn by Albrecht Dürer (De Symmetria... Humanorum Corporum 1525).

We will show that the Dürer twins, once defined in 5-dim space, is a pure merohedral twin, in the sense of Georges Friedel, leaving the 5-dim lattice invariant. This analysis will be generalized to the Cn-modules.

 

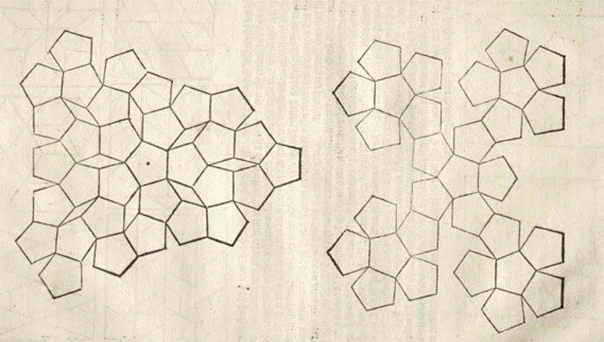
Original drawings of pentagonal structures created by A.  Dürer (De Symmetria... Humanorum Corporum 1525)1525)