Square-triangle tilings: a template for soft-matter quasicrystals
J-F. Sadoc1, R. Mosseri2
1 Laboratoire de Physique des Solides, CNRS-UMR 8502, Bât. 510, Université Paris-sud,
F 91405 Orsay cedex
2Laboratoire de Physique Théorique de la Matière Condensée, UPMC, CNRS UMR 7600,
4 place Jussieu, F-75005 Paris
Jean-francois.sadoc@u-psud.fr
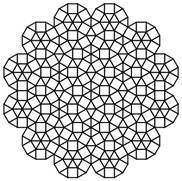
Square and equilateral triangle tilings with twelvefold rotational symmetry are used to model quasicrystals observed in dendrimeric supramolecular liquid crystals [1,2]. First, they have being found in alloys related to Frank-Kasper metallic phases [3] and they can be used to define quasicrystalline Frank-Kasper phases, periodic in one dimension and quasiperiodic in the orthogonal plane.Quasiperiodic tilings can be built using their self-similar properties [4]. But in the case of the square-triangle tiling difficulties occurs mainly due to the fact that this tiling can easily appears as a random tiling with intermediate solutions between the perfect 12-fold quasicrystal and random tiling. They have been described using decoration procedure given by Schottmann described in [5]. We give a simpler method to algorithmically construct the tiling and control the symmetry. They can also be described from cut and project method using a double hexagonal lattice in 4D. In this talk we will compare the two methods and show how the cut and projection method involve fractal acceptance domains of different aspect depending on the choice of a 12-fold symmetry or other possibilities including 6-fold symmetry or random tiling.
We will also discuss the stability of quasicrytalline organisation of nanoparticles covered with a polymeric crown in relation with the Frank-Kasper coordination shells derived from the square-triangle tiling.